
Geometria de coordenadas no
cálculo de poligonais: Interseção
Prof. Dr. Marcelo de Carvalho Alves
Departamento de Engenharia
Universidade Federal de Lavras
Lavras, MG

Introdução
• Quase todos os levantamentos são referenciados
em sistemas de coordenadas planas retangulares,
exceto em levantamentos de controle geodésicos
em extensas áreas.

• As vantagens de referenciar pontos em um
sistema de coordenadas retangulares são: (1) as
posições do ponto são individuais , (2) os pontos
podem ser representados graficamente , (3) no
caso de perda de pontos no campo, os valores
podem ser recuperados a partir de outros pontos
no mesmo sistema de referência, e (4) os cálculos
computacionais são facilitados.
Introdução

• As situações em que se utilizam problemas de
geometria de coordenadas são interseção de
pontos com (a) duas linhas, (b) uma linha e um
círculo e (c) dois círculos.
• Os problemas de interseção podem ser resolvidos
realizando-se triângulos entre duas estações com
posições conhecidas a partir de onde as
observações são realizadas.
Introdução

• Duas importantes funções utilizadas para resolver
triângulos oblíquos são (1) lei dos senos e (2) lei
dos cossenos.
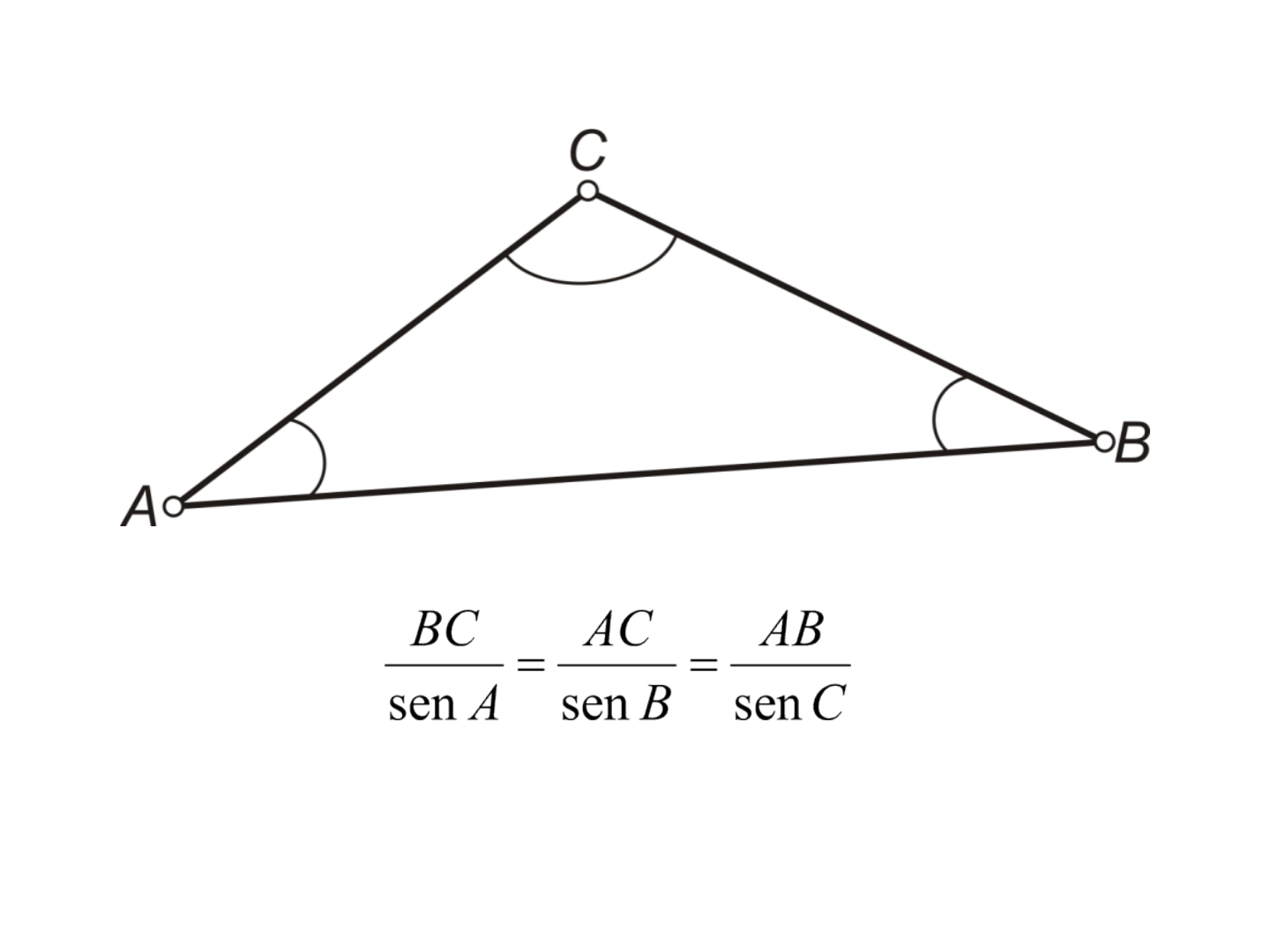
• A lei dos senos relaciona o comprimento dos lados
de um triângulo com o seno de ângulos opostos
Solução de triângulos oblíquos
Solução de triângulos oblíquos
Triângulo oblíquo
em que, AB, BC, e AC são os comprimentos dos três
lados do triângulo ABC, e A, B, e C são os ângulos.
Solução de triângulos oblíquos
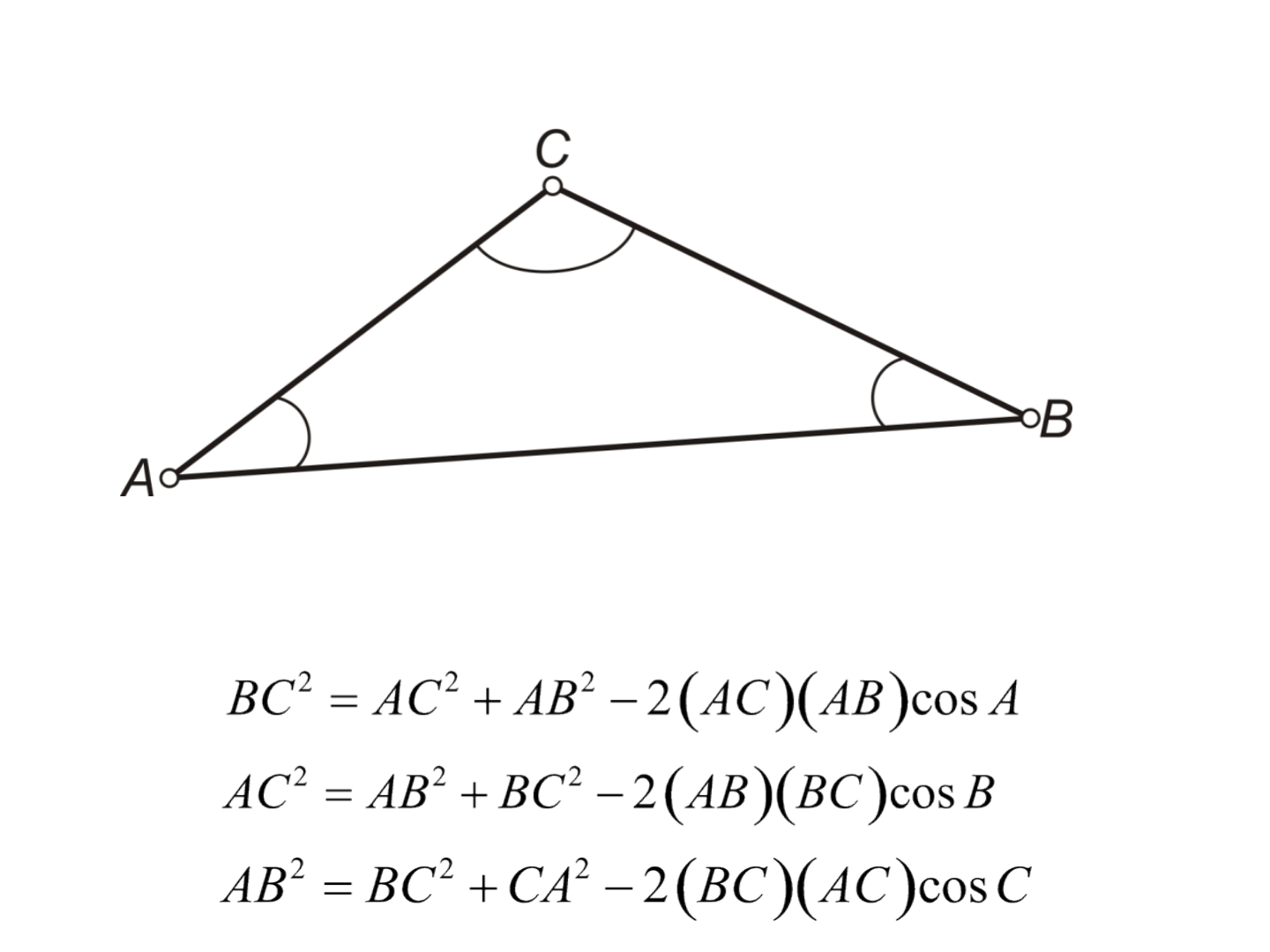
A lei dos cossenos relaciona dois lados e o ângulo
interno com o comprimento do lado aposto ao ângulo:
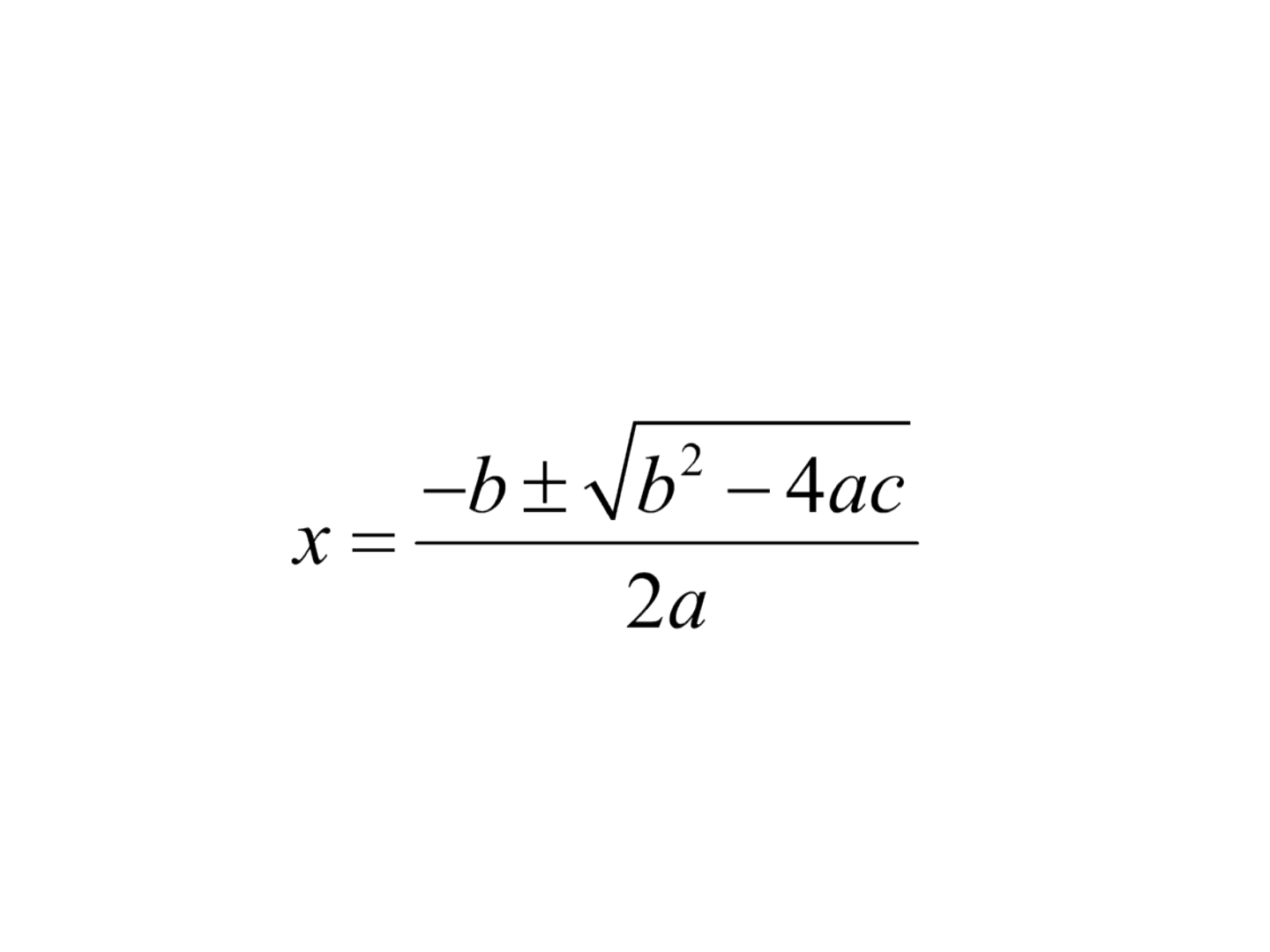
Solução de triângulos oblíquos
A equação que fornece a solução para x em
qualquer equação quadrática ax
2
+ bx + c = 0:
Essas equações podem ser utilizadas para
resolver alguns tipos de problemas de
geometria de coordenadas.

Equações de coordenadas para linhas e círculos
• Um alinhamento AB reto pode ser referenciado
em um sistema de coordenadas planas.
• As coordenadas dos pontos A e B das
extremidades são X
A
, Y
A
, e X
B
, Y
B
,
respectivamente.
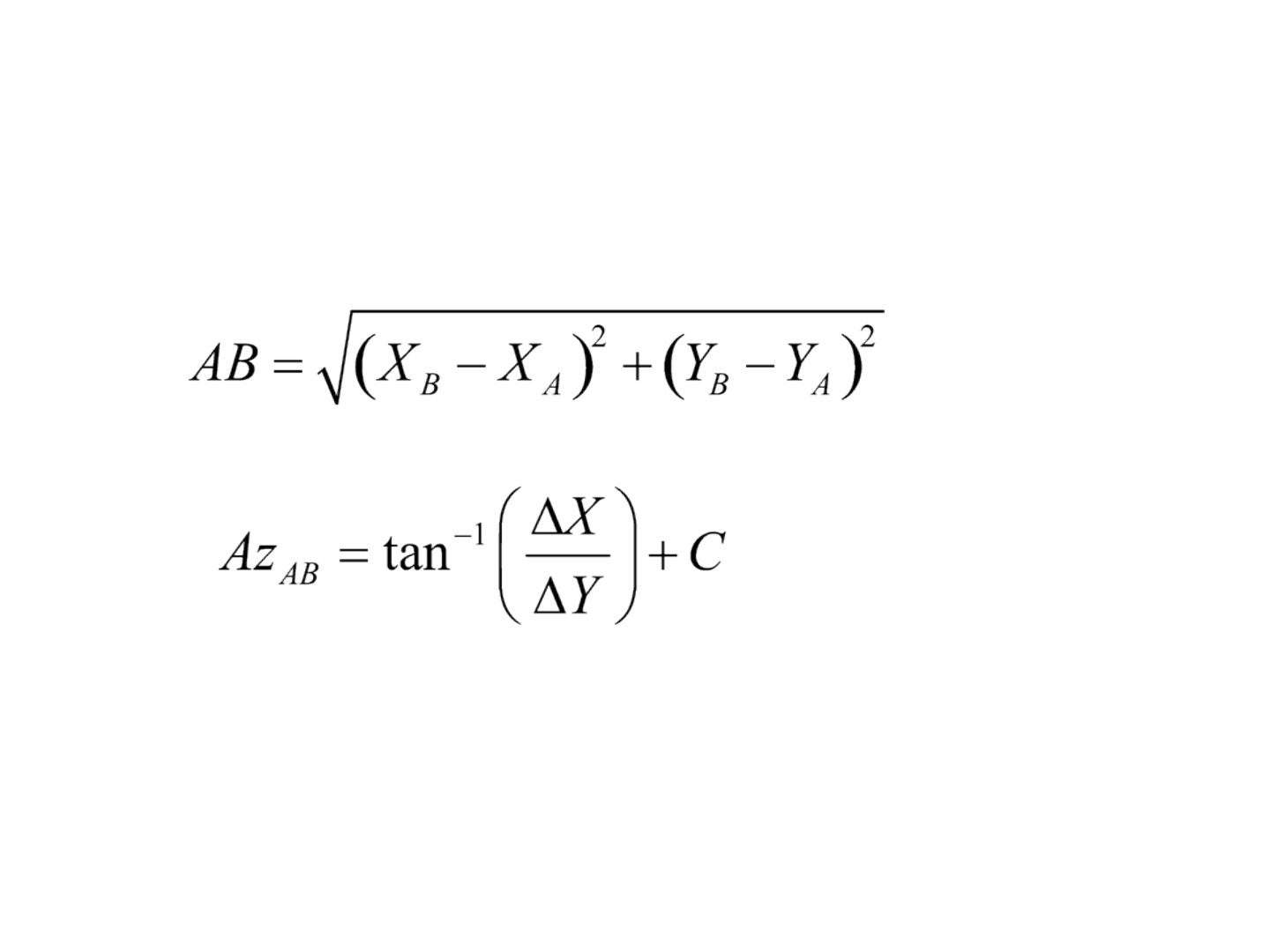
Equações de coordenadas para linhas e círculos
• O comprimento AB e o azimute Az
AB
dessa linha
com base em coordenadas são:
em que, ΔX é X
B
- X
A
, ΔY é ΔY
B
- ΔY
A
, C é 0
o
se ambos
ΔX e ΔY forem maiores do que 0; 180º se ΔY for
menor do que 0; e 360º se ΔX for menor do que 0
e ΔY maior do que 0.
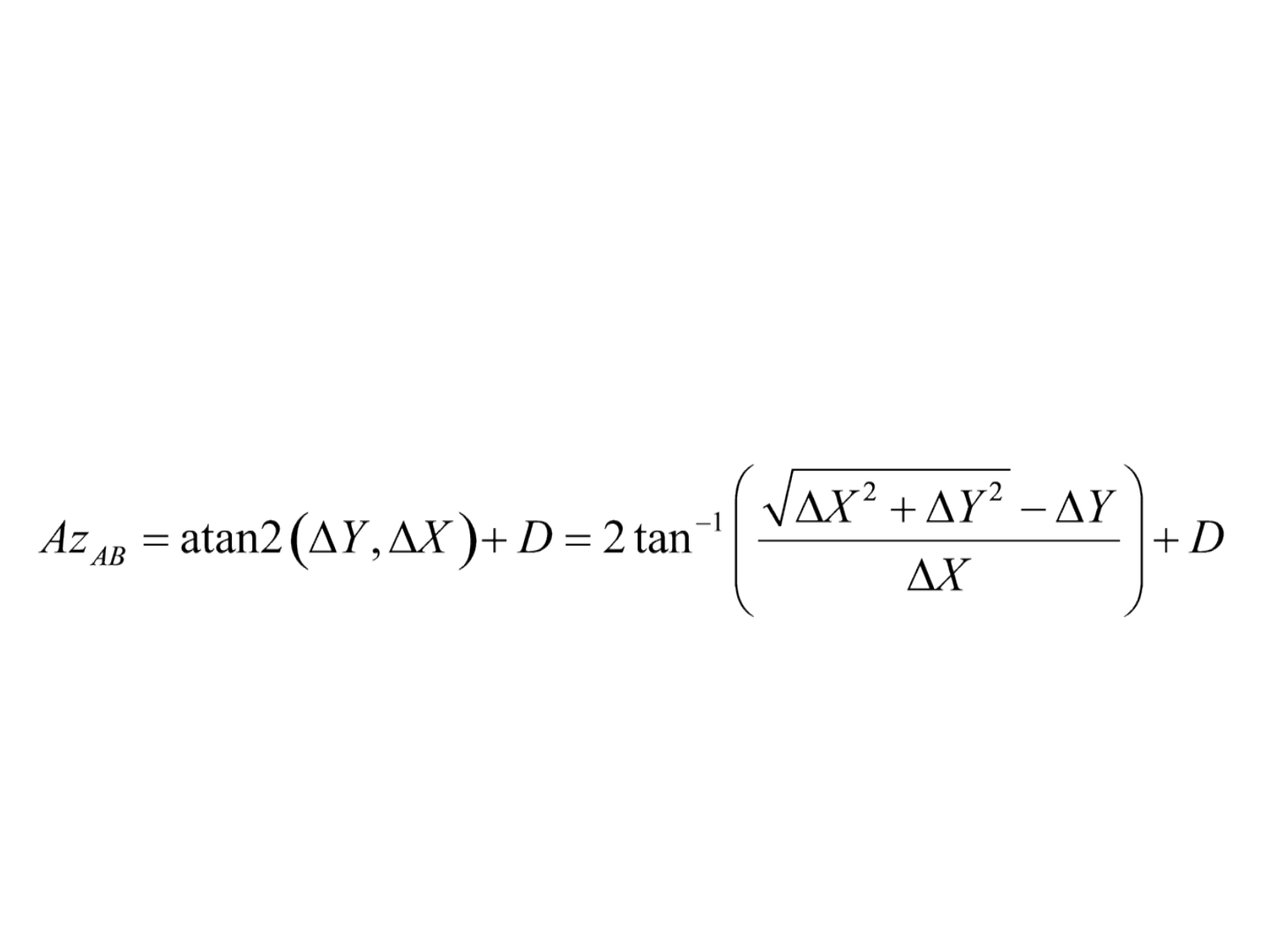
Equações de coordenadas para linhas e círculos
• Outra equação utilizada para determinar o azimute
de um alinhamento em programas de computador
é conhecida como a função tan2:
em que, D é 0
o
se o resultado da função atan2 é
positivo e 360º se o resultado é negativo.
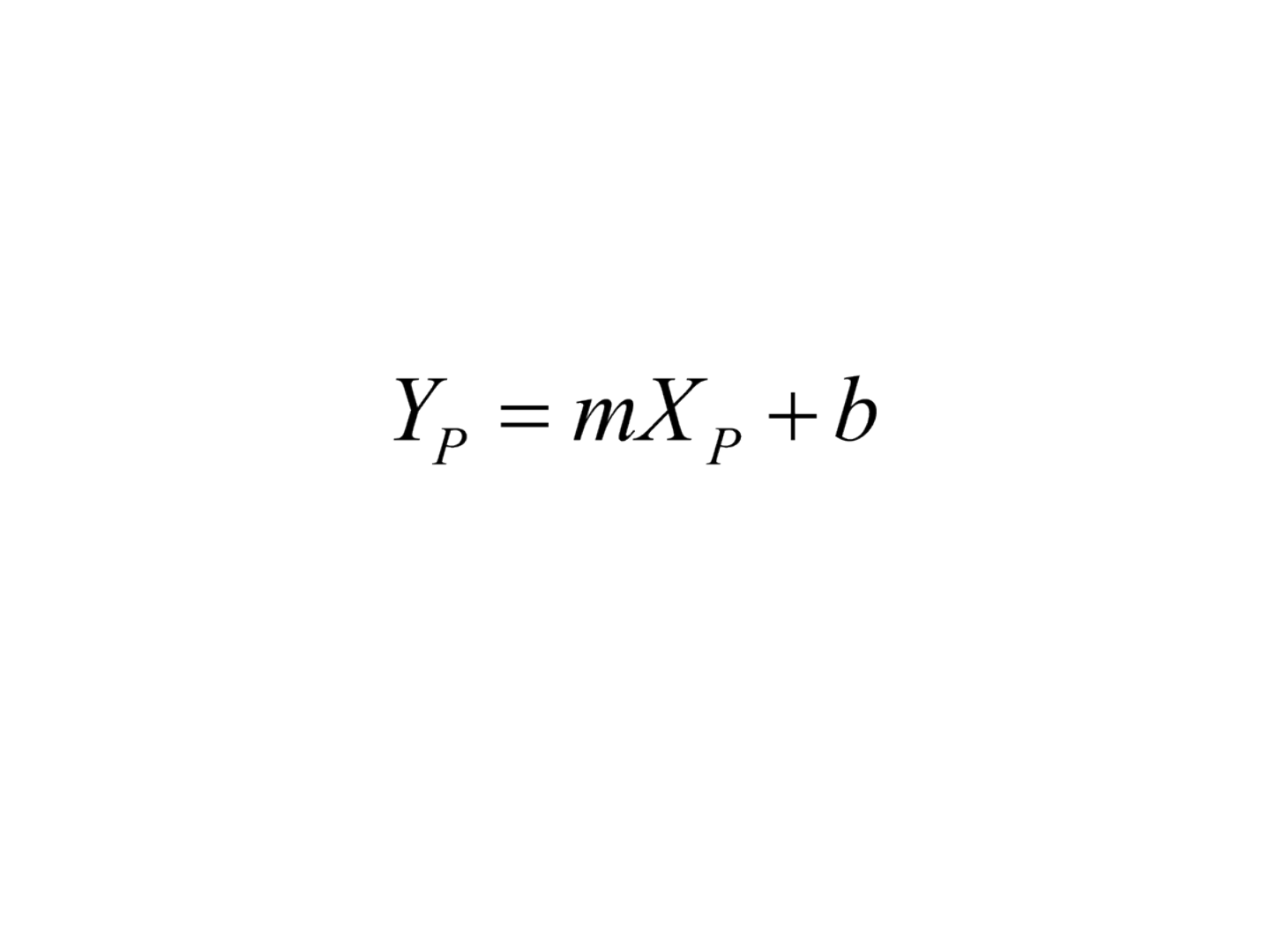
Equações de coordenadas para linhas e círculos
• A expressão matemática geral para uma linha reta
é:
em que, Y
P
é a coordenada Y de qualquer ponto P na
linha cuja coordenada X é X
P
, m é a declividade da
linha e b, o intercepto y da linha.
Equações de coordenadas para linhas e círculos
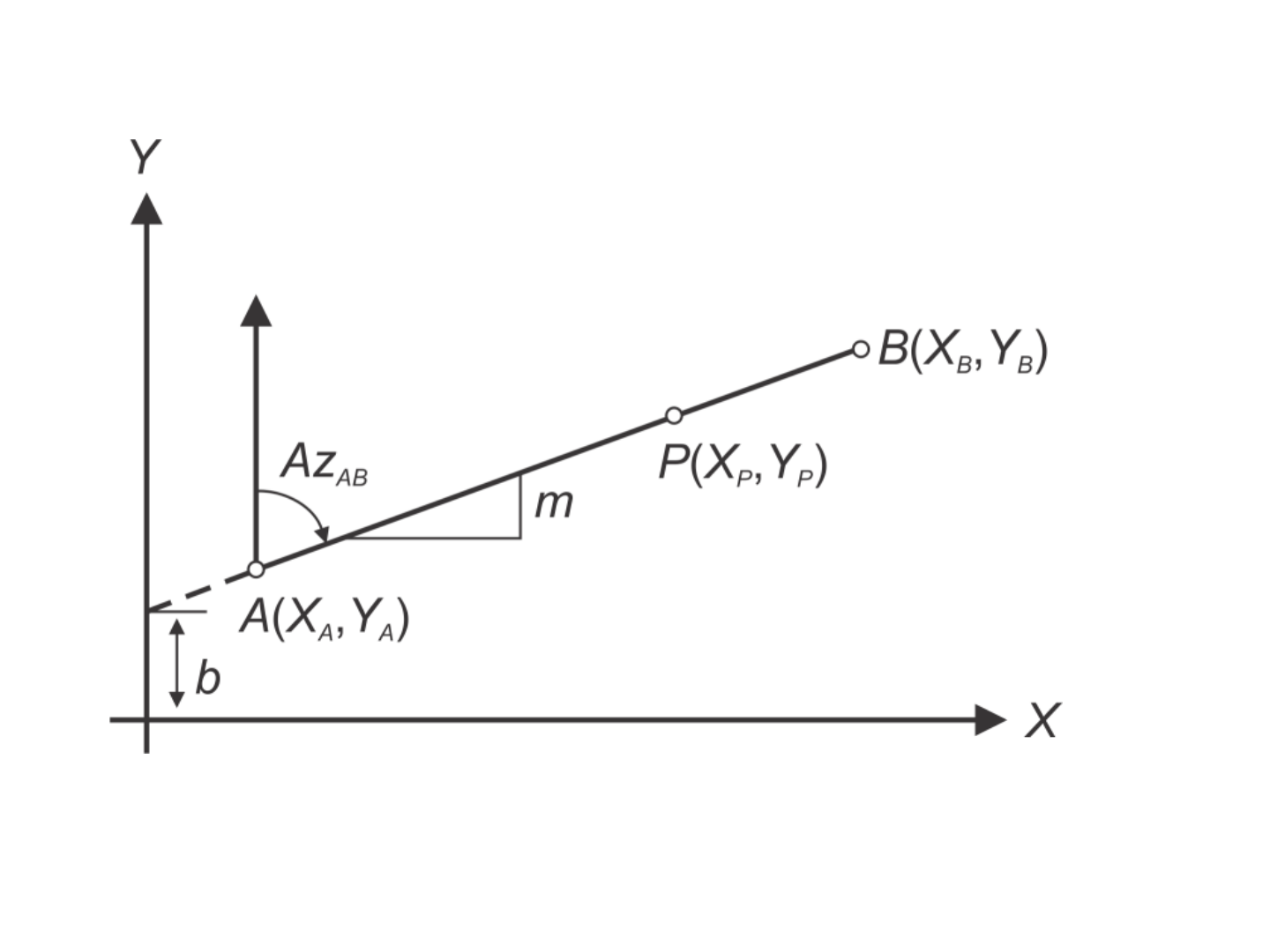
Geometria de coordenadas de uma linha reta
em um sistema de coordenadas planas
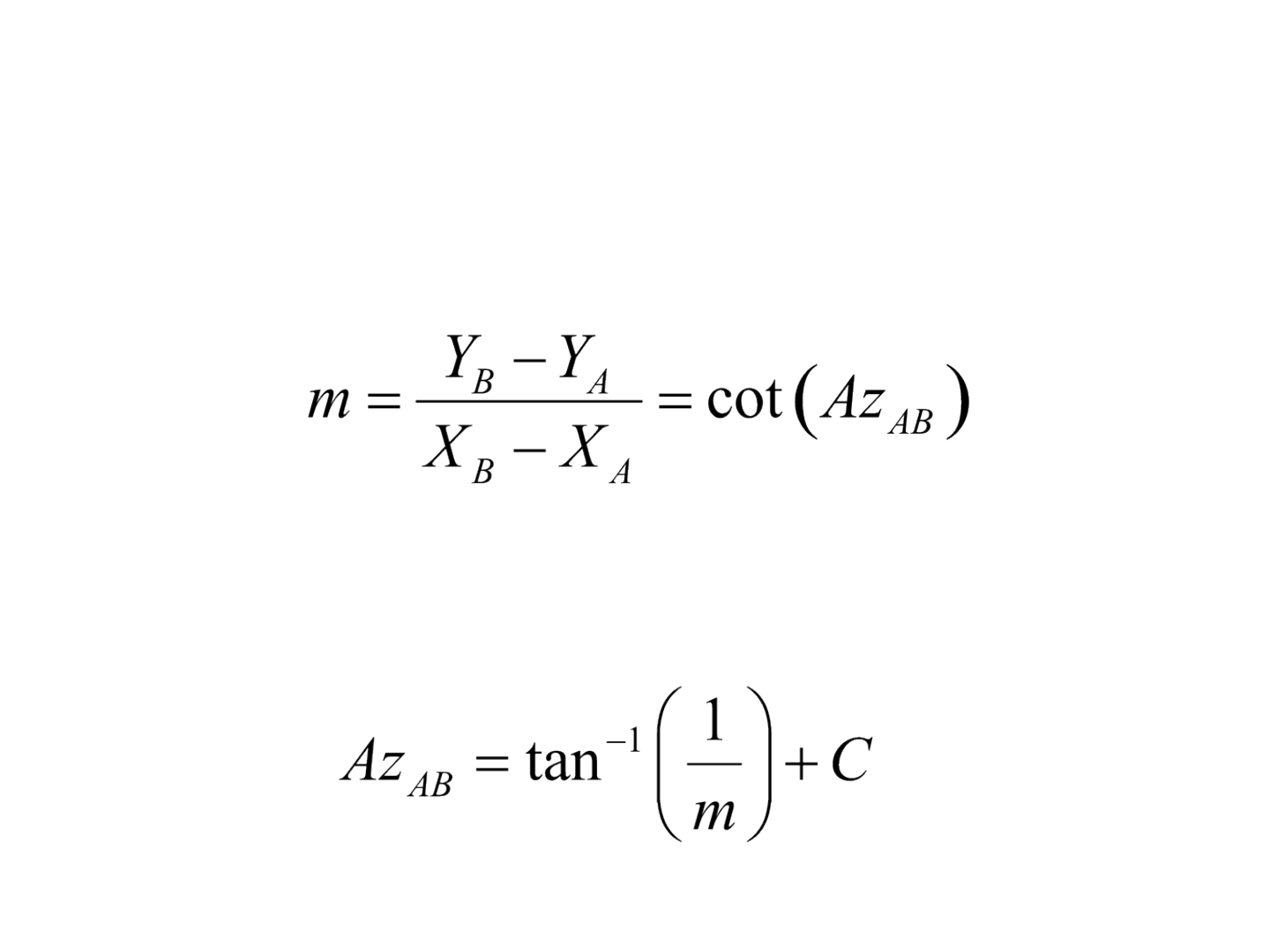
Equações de coordenadas para linhas e círculos
• A declividade m pode ser descrita por:
• Assim, pode-se observar que:
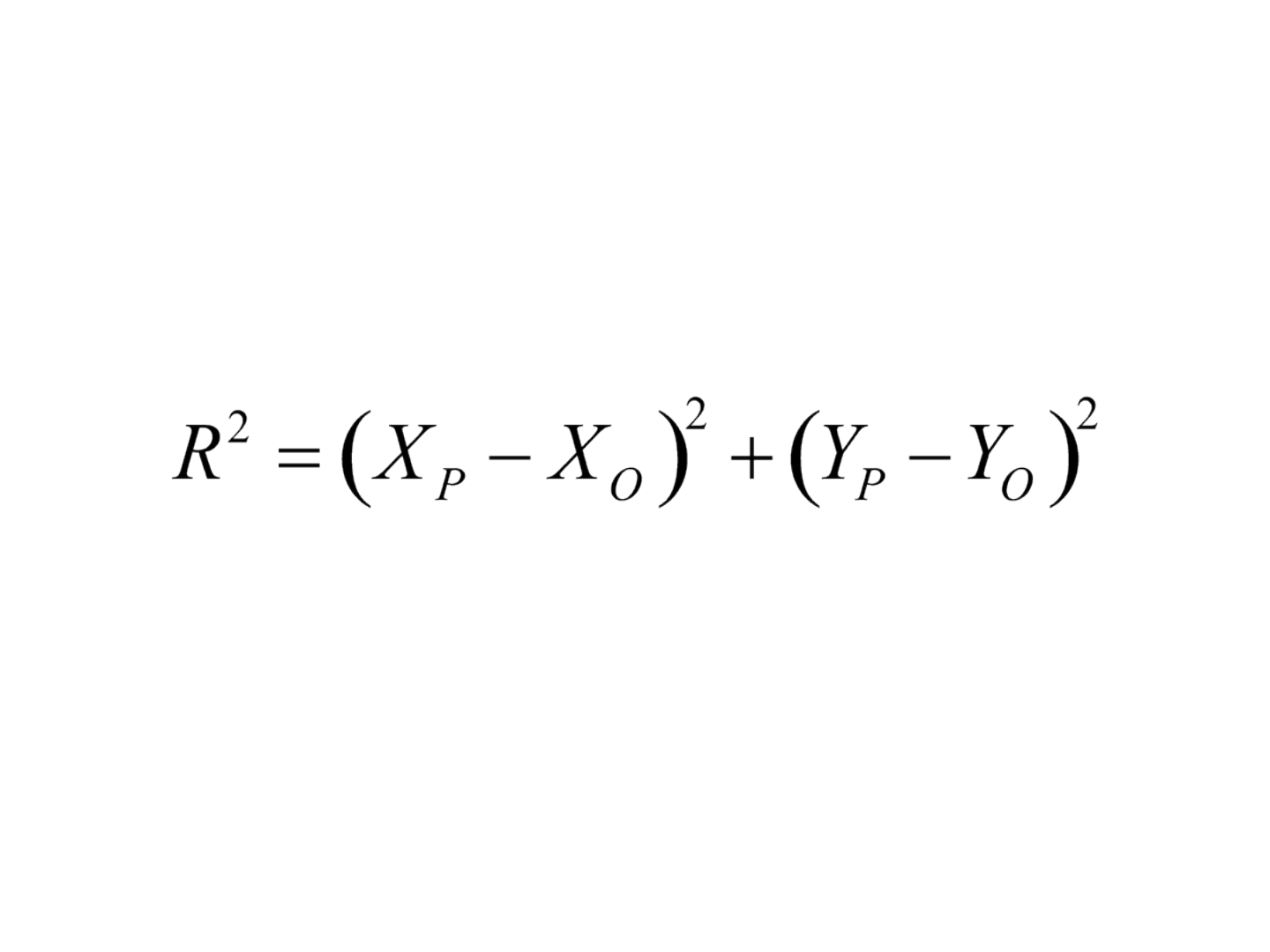
Equações de coordenadas para linhas e círculos
• A equação matemática para caracterizar um círculo
com coordenadas retangulares é:
em que, R é o raio do círculo, X
O
e Y
O
são as
coordenadas do ponto do raio O , e X
P
e Y
P
são as
coordenadas de qualquer ponto P no círculo.
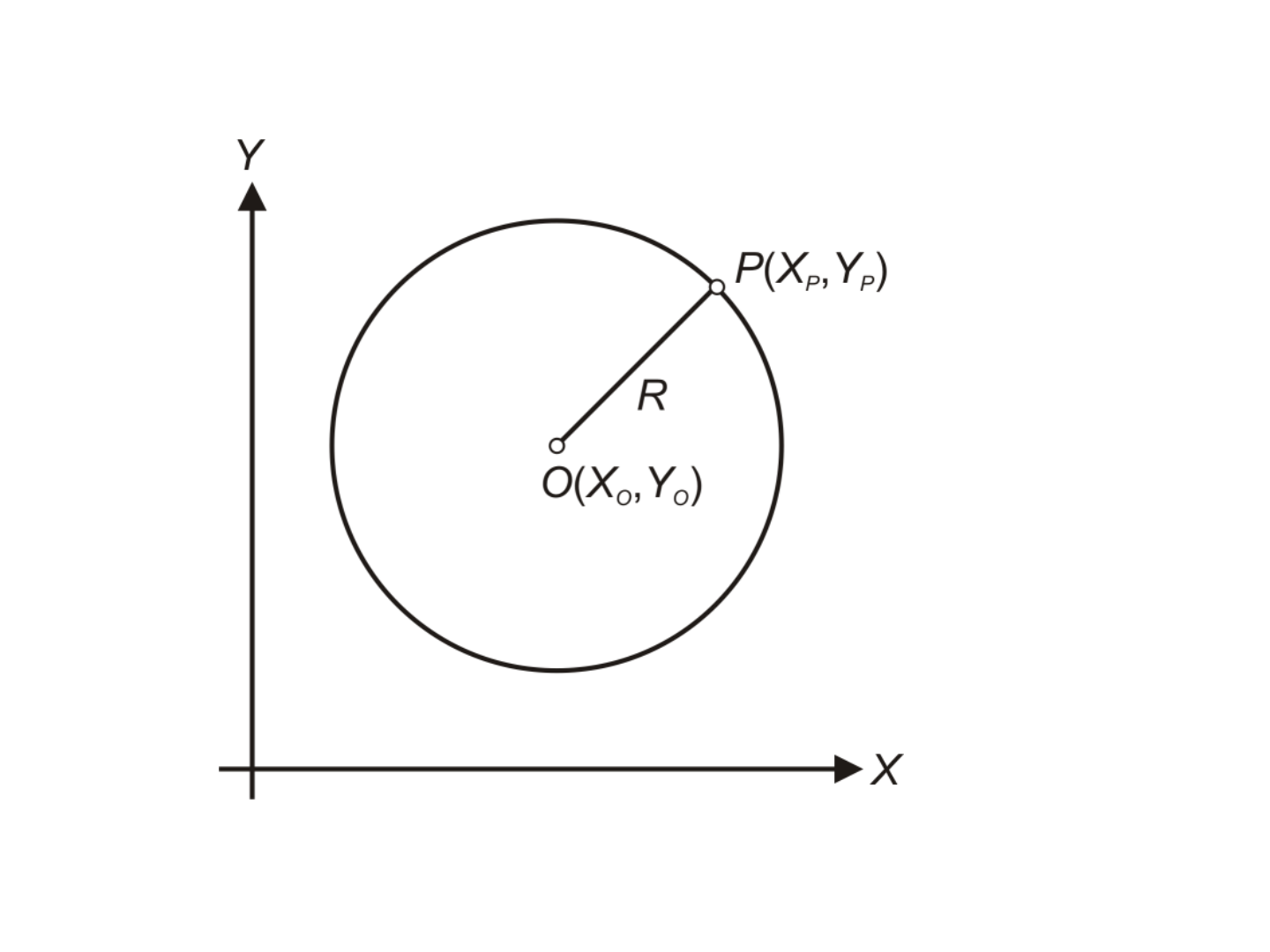
Equações de coordenadas para linhas e círculos
Geometria de um círculo em um sistema de coordenadas
planas
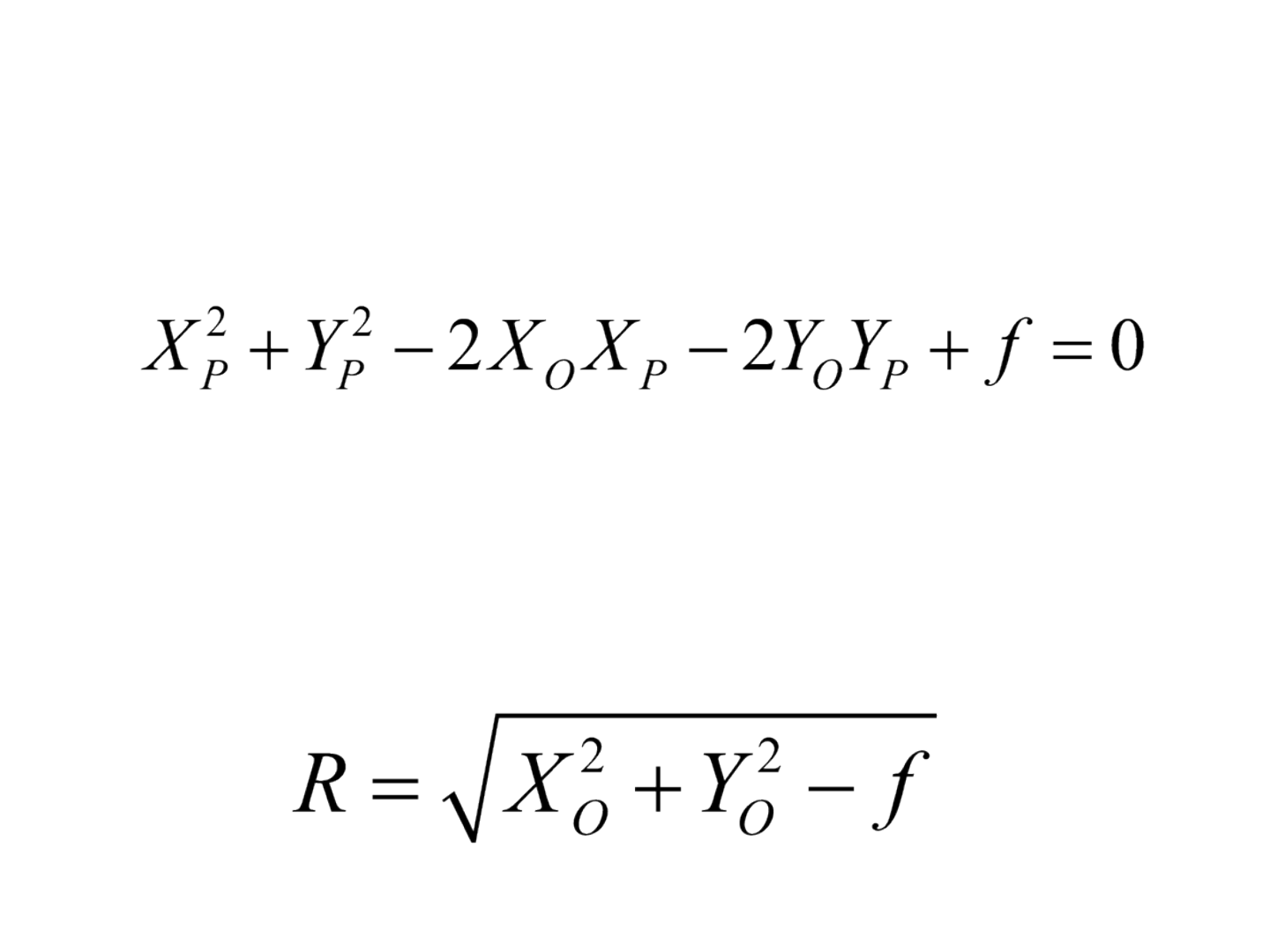
Equações de coordenadas para linhas e círculos
• Outra forma de representar a equação do círculo é:
em que, o comprimento do raio do círculo é
determinado por: