
Poligonação e geometria de
coordenadas em levantamentos:
Caminhamento
Prof. Dr. Marcelo de Carvalho Alves
Departamento de Engenharia
Universidade Federal de Lavras
Lavras, MG

Introdução
• As poligonais fechadas retornam ao ponto inicial
formando uma figura geometricamente e
matematicamente fechada.
• Poligonais fechadas possibilitam checar os
ângulos e distâncias observados e são utilizadas
em controle, construção, propriedades e
levantamentos topográficos.

Observação de ângulos e direções
em poligonais
• Os ângulos ou direções de linhas de poligonais
podem ser observados por métodos de (1)
ângulos internos, (2) ângulos externos, (3)
ângulos de deflexão e (4) azimutes.

Poligonais por ângulos internos
• Os ângulos devem sempre ser lidos no sentido
horário da estação de ré para a estação de vante
• Para reduzir enganos em leitura, registro e
cálculo, recomenda-se o caminhamento na área
no sentido anti-horário.

Poligonais por ângulos externos
• São semelhantes às poligonais por ângulos
internos, no entanto, caminha-se no terreno pelo
sentido horário, medindo-se os ângulos externos
do polígono.

Poligonais por ângulos de deflexão
• Utilizado em levantamentos de rotas observados à
direita ou à esquerda de linhas.
• Um ângulo de deflexão não está completo sem a
indicação para direita ou esquerda do curso e não
deve exceder 180º.
• Valores positivos e negativos configuram ângulos
de deflexão para direita e esquerda,
respectivamente.
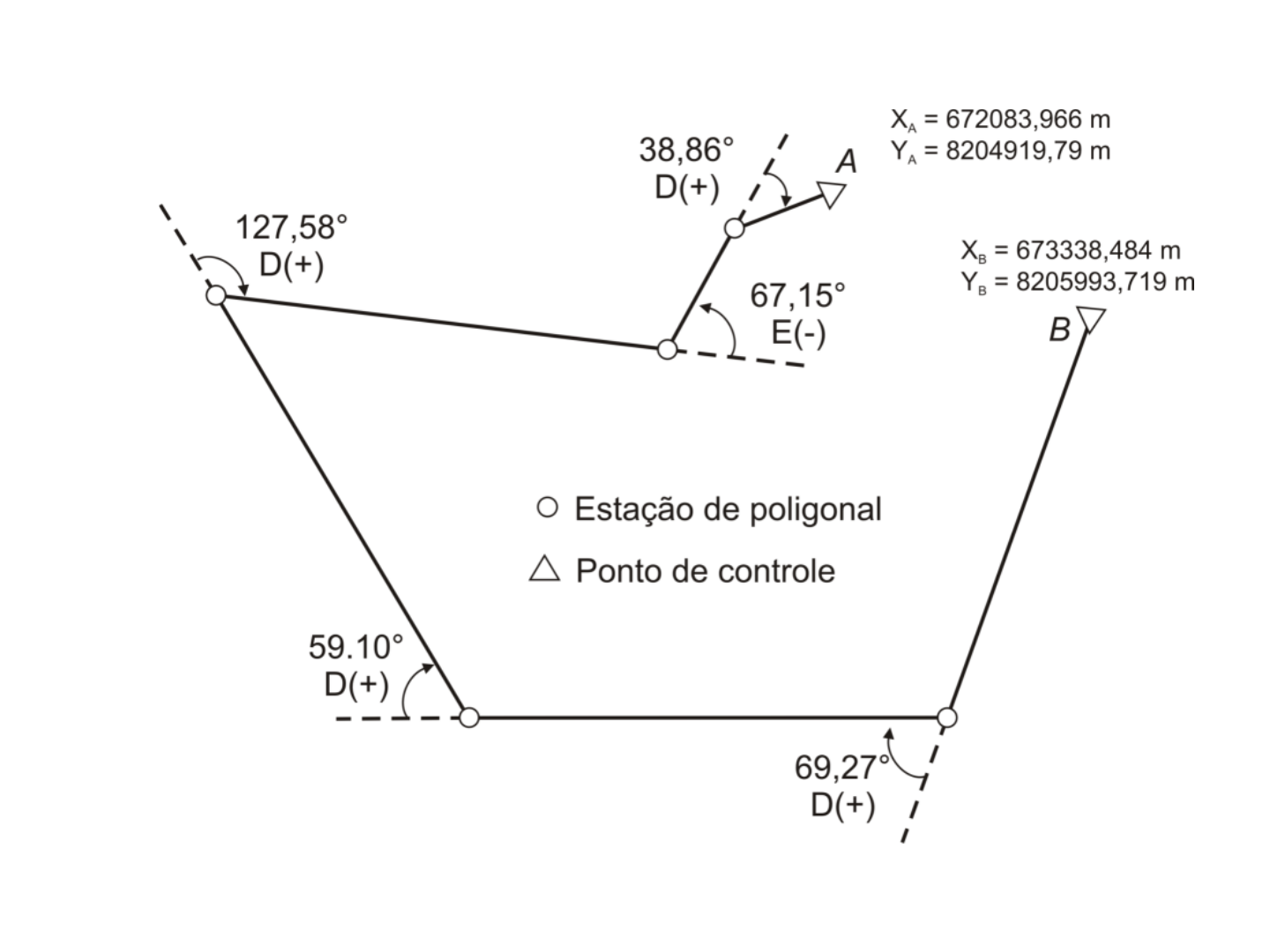
Poligonais por ângulos de deflexão
Poligonal aberta apoiada em nos pontos de controle A e B levantada na Fazenda Boa
Vista, Mato Grosso, Brasil.

Poligonais por azimutes
• Esse processo possibilita ler os azimutes de todas
as linhas diretamente eliminando a necessidade de
calculá-los.
• A diferença entre o primeiro e último azimute lido
é o erro angular de fechamento.
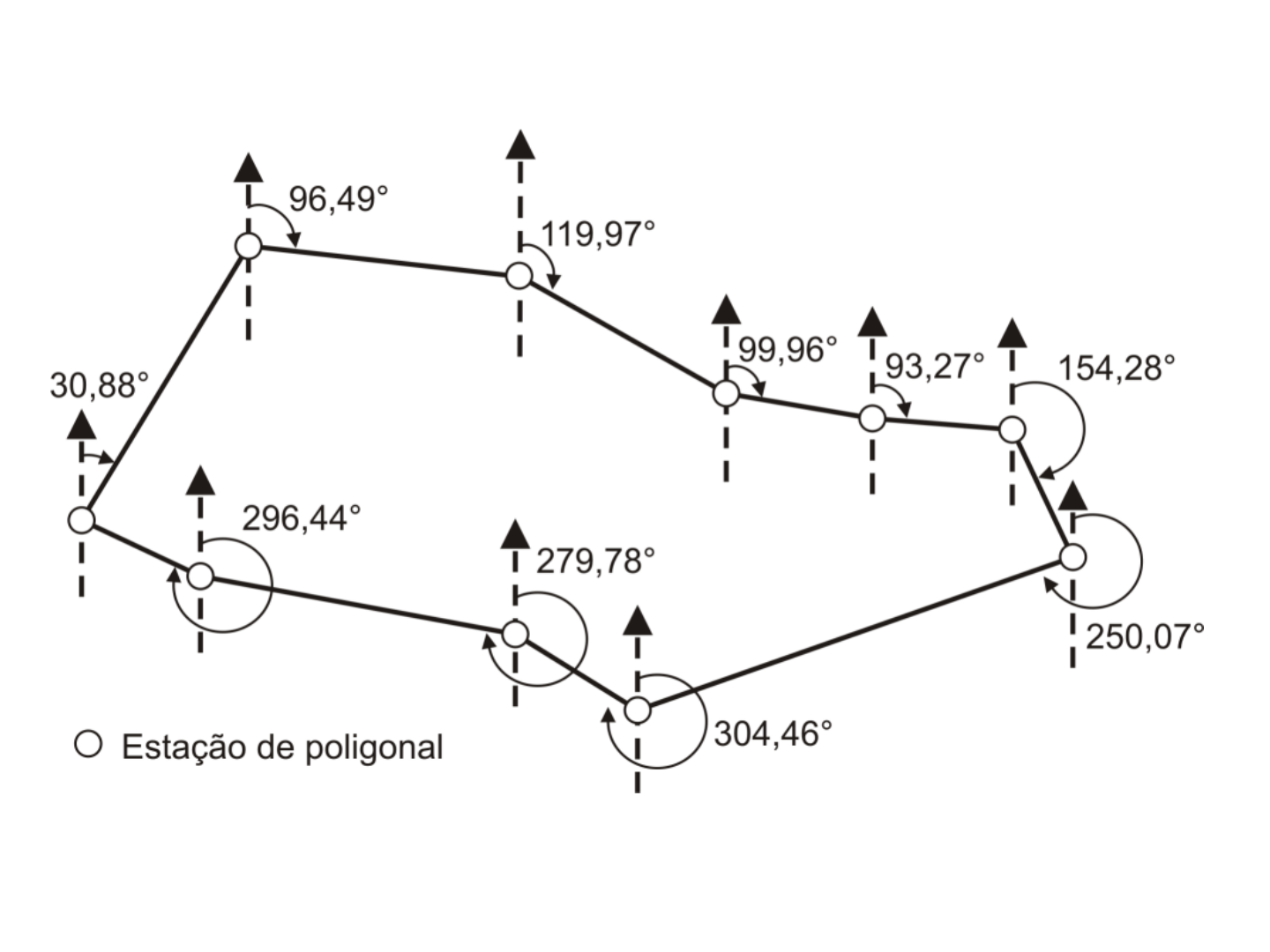
Poligonais por azimutes
Poligonal por azimute utilizada para demarcar a área de reserva legal da Fazenda
Boa Vista 2 em Santo Antônio do Leveger, Mato Grosso, Brasil.

Observação de comprimento de
poligonais
• O comprimento de cada linha de poligonal deve
ser medido pelo método mais simples e
econômico que satisfaça a precisão requerida pelo
projeto.
• A média de distâncias de visada de vante e de ré
pode aumentar a acurácia do levantamento

Seleção de estações de poligonais
• As estações devem ser localizadas em pontos de
fácil acesso.
• O número de estações pode ser reduzido com um
cuidadoso reconhecimento da área.
• No levantamento de propriedades, as estações são
colocadas em cada vértice.
• Em alguns casos é necessário considerar um valor
de afastamento de uma estaca próxima ao vértice.

Referênciamento de estações de
poligonais
• Estações de poligonais podem ser reocupadas
após sua construção.
• No entanto, é importante criar pontos de
observação de amarração no caso de destruição
ou novas construções.

Cálculo de poligonais
• Os ângulos e direções obtidas na medição de
poligonais fechadas podem ser avaliados após o
término do trabalho de campo.
• Após a determinação dos erros das medidas
lineares e angulares, a poligonal pode ser ajustada
a fim de se determinar um fechamento com
consistência geométrica entre ângulos e
comprimentos.

Cálculo de poligonais
• Dependendo da magnitude do erro, as
observações de campo devem ser repetidas até se
obter resultados adequados.
• A determinação da precisão do ajustamento é
extremamente importante para avaliar se o
mapeamento da propriedade está dentro das
especificações determinadas por lei

Cálculo de poligonais
• Diferentes procedimentos podem ser utilizados
para calcular e ajustar poligonais.
• Esses procedimentos variam desde métodos
elementares até técnicas mais avançadas baseadas
no método de mínimos quadrados. Apenas
procedimentos elementares serão considerados
neste capítulo.

Cálculo de poligonais
• Os passos básicos de cálculo de poligonais são: (1)
ajuste de ângulos para fixar condições geométricas,
(2) determinação de azimutes (ou rumos) dos
alinhamentos, (3) cálculo de longitude e latitude e
ajuste do erro de fechamento , (4) cálculo de
coordenadas retangulares das estações de poligonal
e (5) cálculo dos comprimentos e azimutes das linhas
de poligonal após o ajustamento.
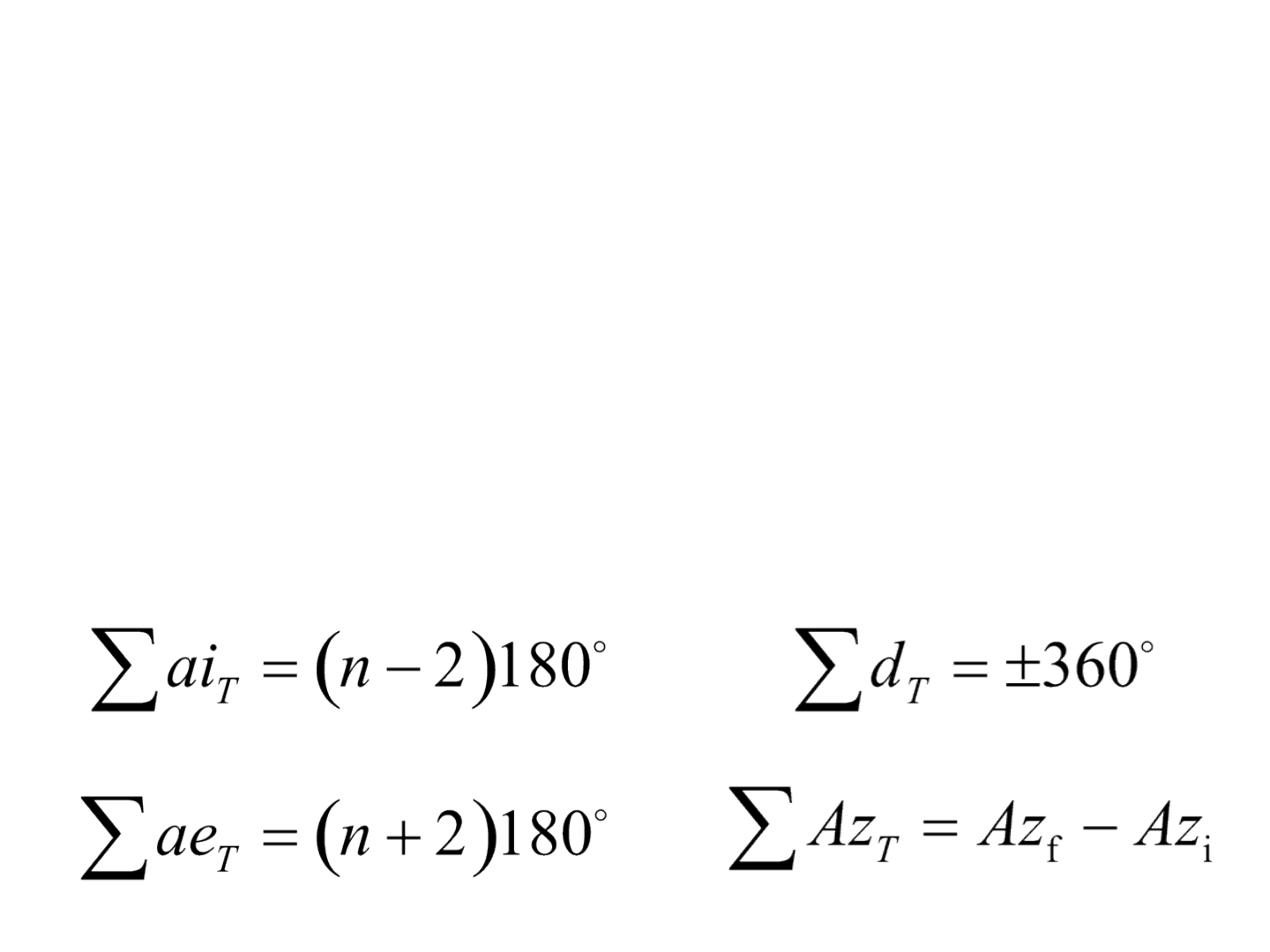
Balanceamento de ângulos
• É realizado a partir do conhecimento do erro total da
somatória de ângulos da poligonal.
• O erro angular pode ser determinado em função do valor
esperado ou teórico da somatória dos ângulos que a
poligonal deveria ter.
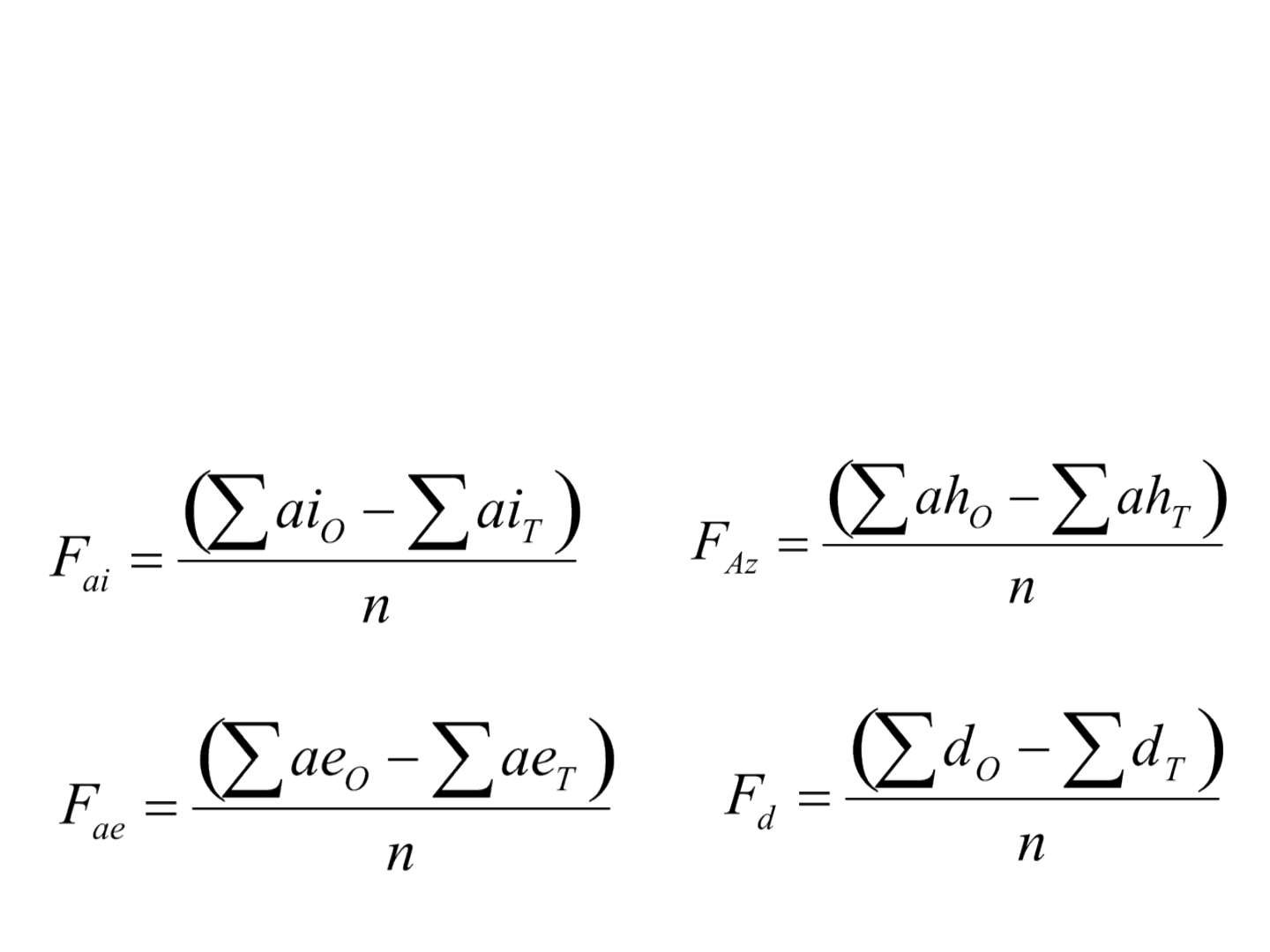
Balanceamento de ângulos
• O erro de fechamento angular a ser distribuído para
cada vértice de estação do levantamento por ângulos
internos (F
ai
), externos (F
ae
), azimutes (F
Az
) e ângulos de
deflexão (F
d
) é calculado por: (*
O
= observado)

Balanceamento de ângulos
• O erro deve ser distribuído em parcelas iguais para
o número total de ângulos medidos, considerando
-se que a correção sempre terá sinal contrário ao
sinal do erro.
• Por exemplo, se a soma dos ângulos medidos
(observados) for maior do que o valor esperado
(teórico), o erro será positivo e, portanto, deve-se
subtrair a correção para cada vértice.

Cálculo de azimutes ou rumos
• Essa etapa requer pelo menos um valor de direção
de um vértice da poligonal, para atribuir a direção
de norte à poligonal.
• Em alguns levantamentos, o rumo magnético de
um alinhamento pode ser determinado e utilizado
como referência de direção, no entanto, para o
levantamento de divisas, são necessárias as
direções verdadeiras.

Cálculo de azimutes ou rumos
• Nesse caso, a direção verdadeira pode ser obtida
(1) incorporando na poligonal uma linha com a
direção verdadeira, (2) realizando observações
astronômicas para determinar a declinação
magnética, ou (3) utilizando GNSS.
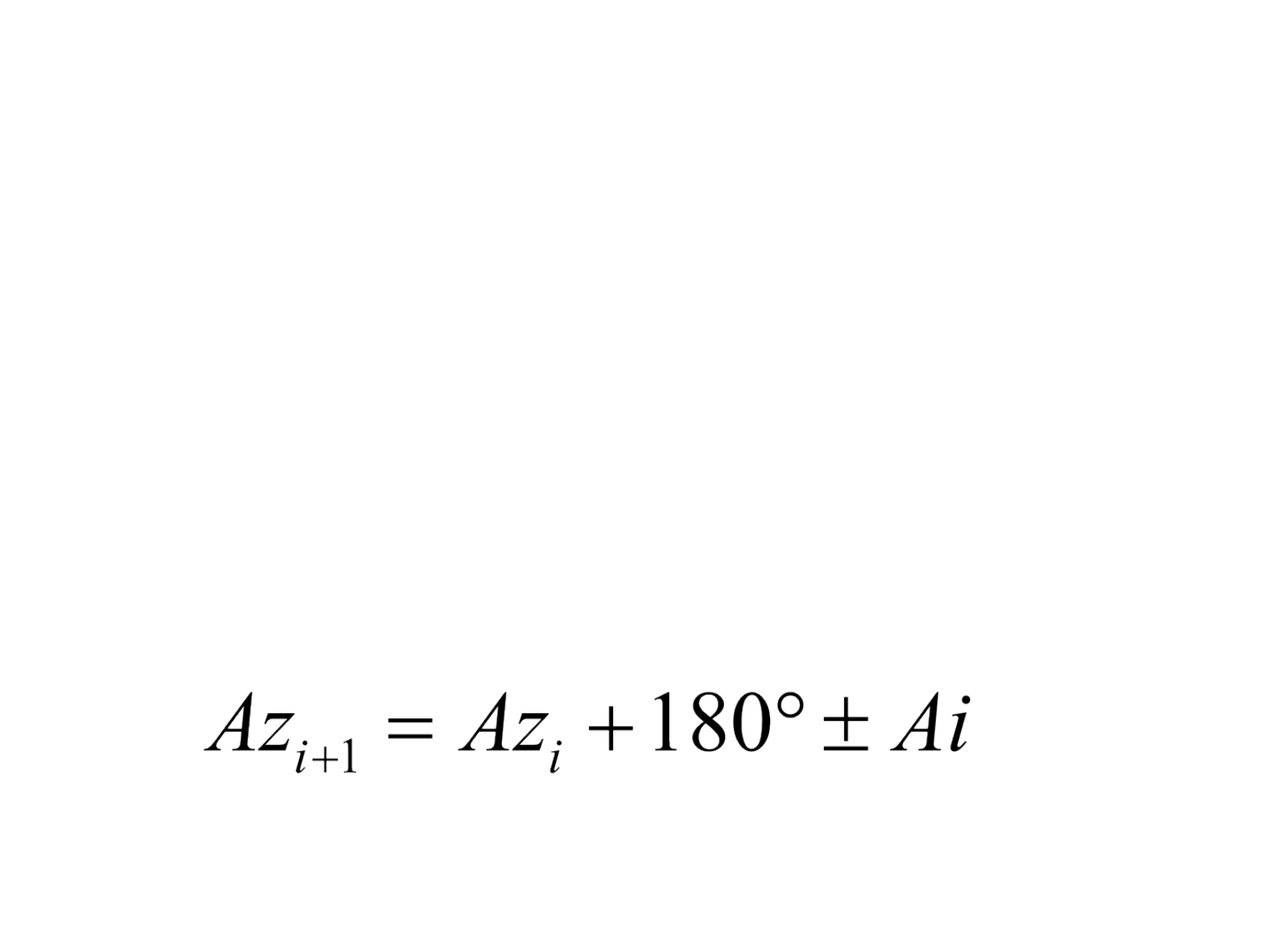
Cálculo de azimutes ou rumos
• Considerando a obtenção de um azimute inicial
obtido de uma rede de referência geodésica ou
determinado em campo, os azimutes dos outros
vértices podem ser calculados em função dos
ângulos internos conhecidos:

Cálculo de azimutes ou rumos
• Se o resultado da equação for negativo, deve-se
somar 360º, e se for maior que 360º, deve-se
subtrair 360º quantas vezes forem necessárias.
• O sinal (+) deve ser utilizado quando o ângulo
entre os alinhamentos for medido no sentido
horário, a partir do alinhamento à ré, caso
contrário, deve-se utilizar o sinal (-).
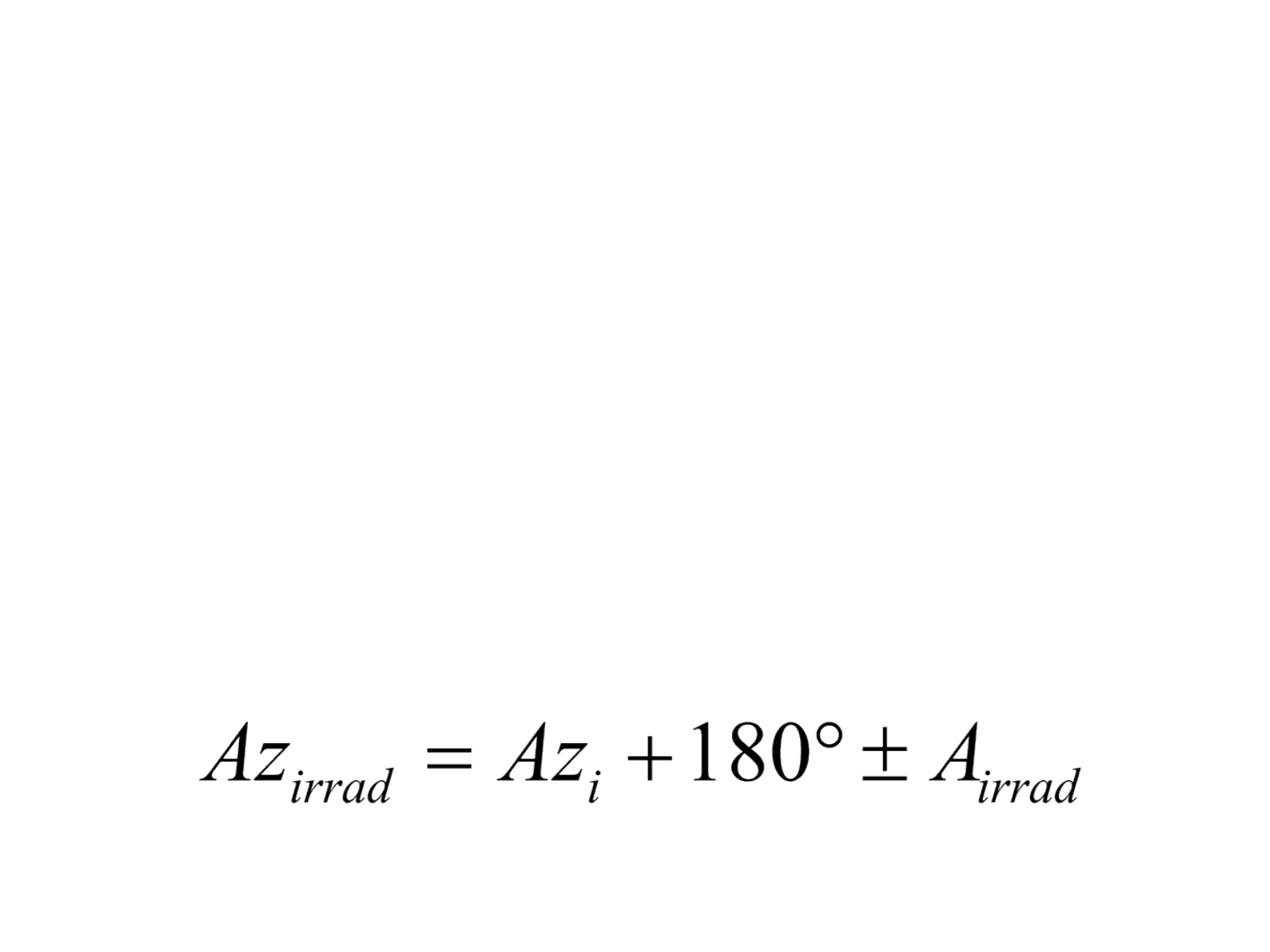
Cálculo de azimutes ou rumos
• No caso de uma poligonal com inclusão de pontos
de detalhes, deve-se calcular o azimute do ponto
irradiado, para que o mapeamento seja
apresentado na mesma direção.
• O azimute da irradiação pode ser calculado por:
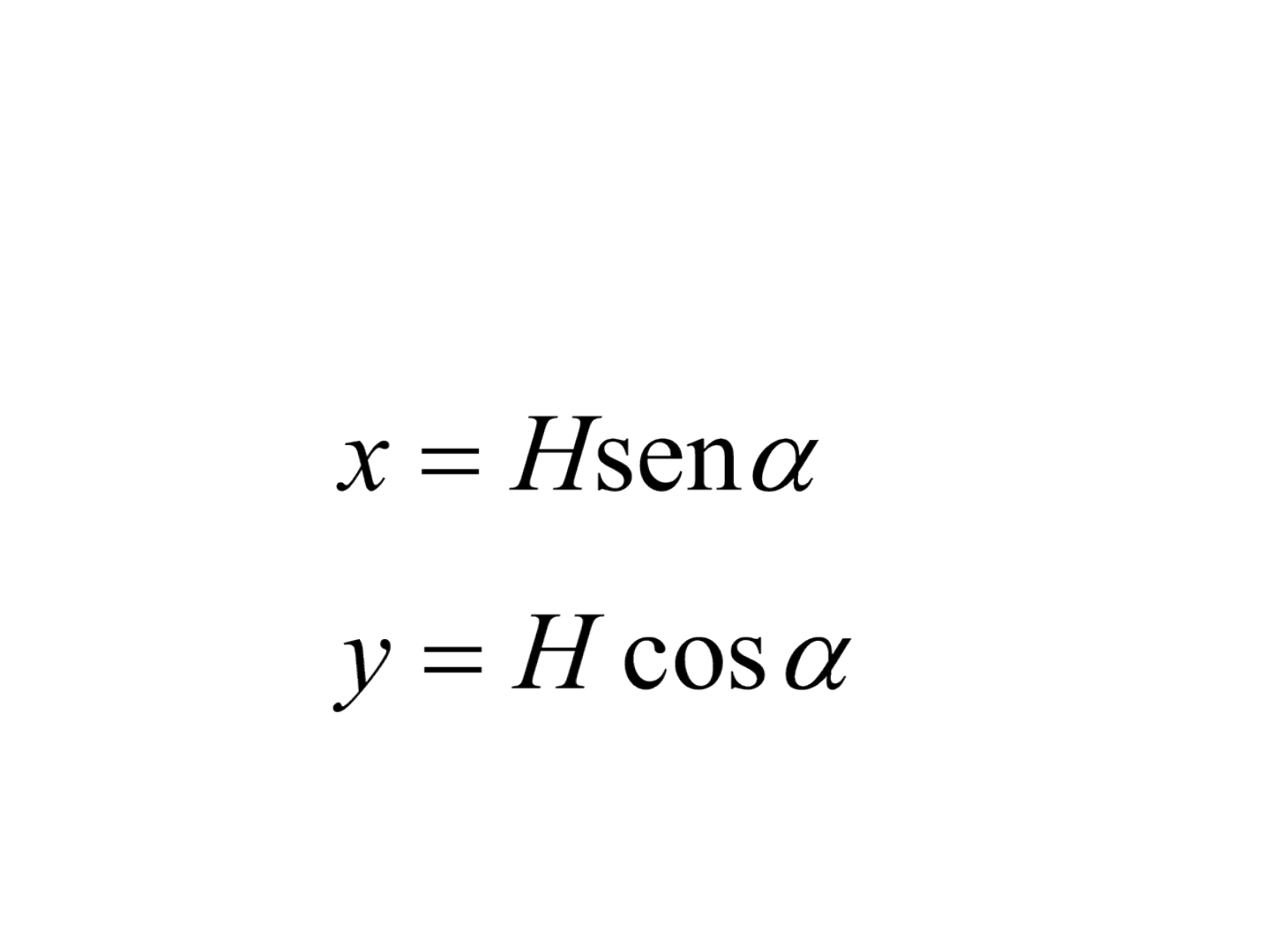
Cálculo de latitude e de longitude
• A longitude (x) e a latitude (y) de uma linha podem
ser obtidas por:

Condições de fechamento de latitude
e de longitude
• Considerando uma poligonal fechada, se todos os
ângulos e distâncias fossem medidos
perfeitamente, a soma algébrica das longitudes de
todos os alinhamentos da poligonal deveria ser
igual a zero.
• A mesma condição se aplica para a soma algébrica
de todas as latitudes.

Condições de fechamento de latitude
e de longitude
• No caso de uma poligonal apoiada , a soma
algébrica das longitudes deveria ser igual à
diferença total da longitude entre os pontos de
controle inicial e final.
• A mesma situação deve ser observada para a
latitude em uma poligonal apoiada.

Condições de fechamento de latitude
e de longitude
• A diferença entre o valor observado e o esperado
determina o erro de fechamento de longitude e o
erro de fechamento de latitude.
• Esses valores são determinados pela soma
algébrica das longitudes e das latitudes, os quais
são comparados com os padrões requeridos.
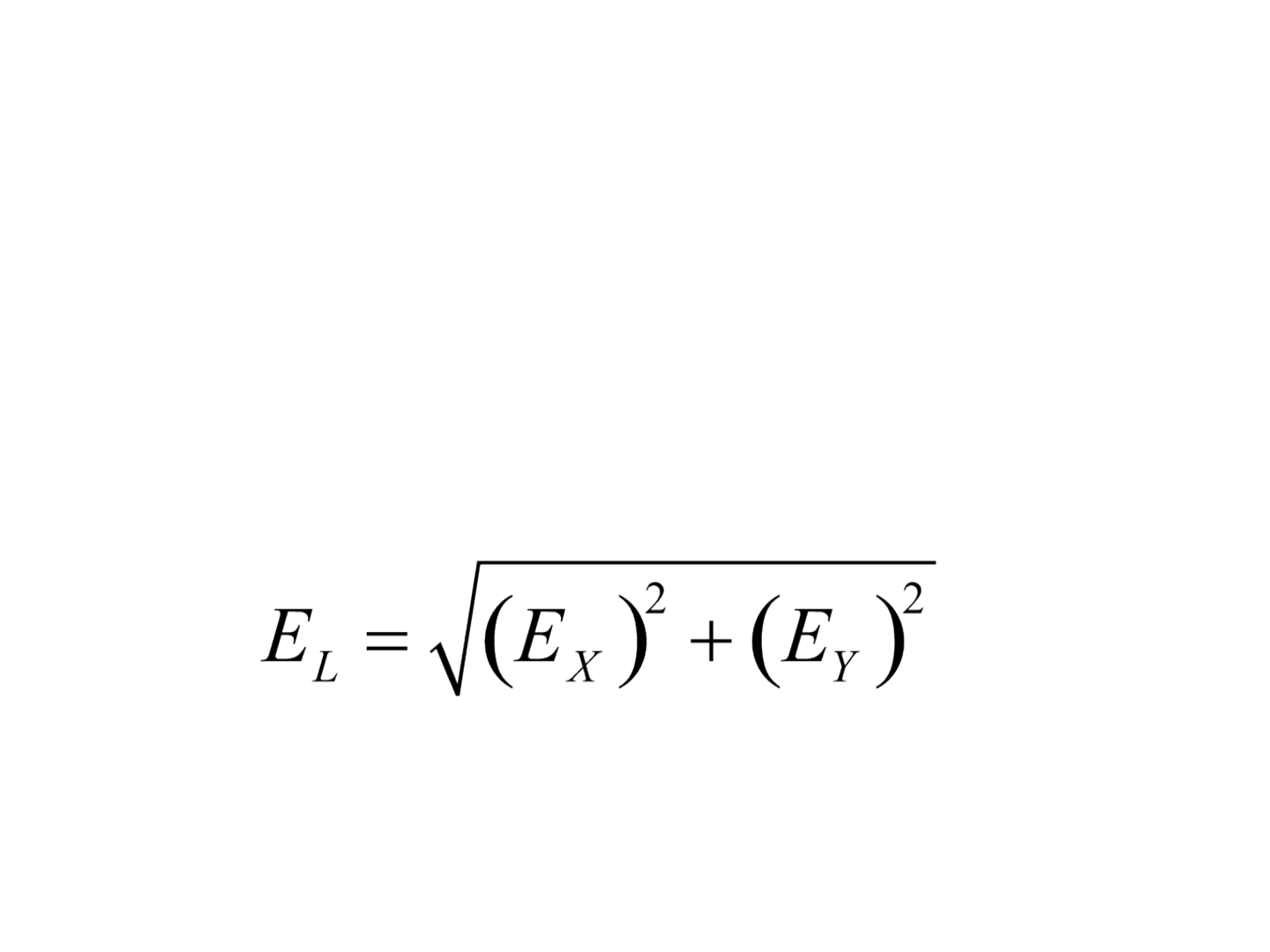
Erro de fechamento linear e precisão
relativa
• Os erros de fechamento de longitude e de latitude
determinam o erro de fechamento linear (E
L
) da
poligonal com base na seguinte equação:
em que E
X
é o erro de fechamento da longitude e E
Y
,
o erro de fechamento da latitude.
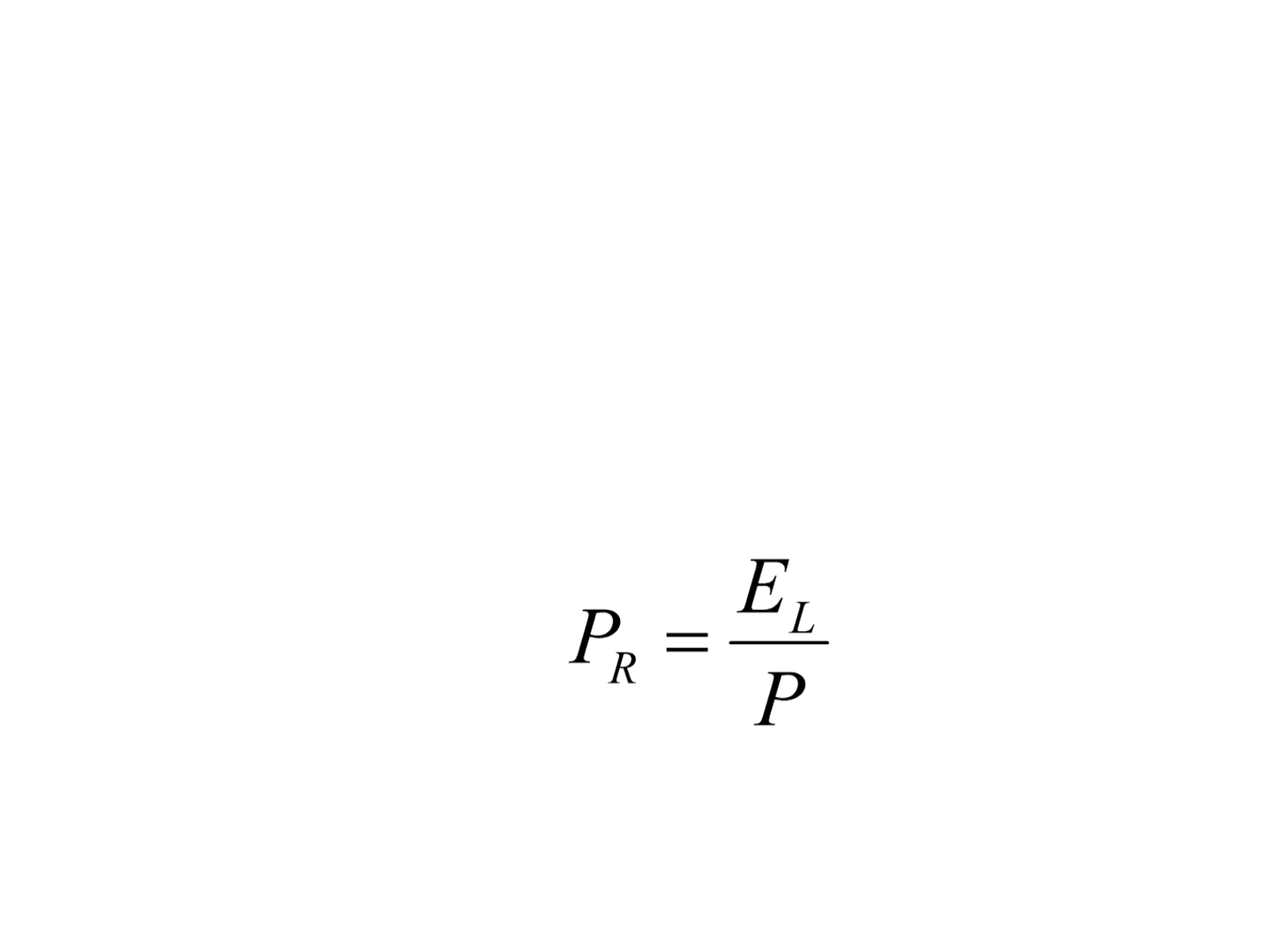
Erro de fechamento linear e precisão
relativa
• A precisão relativa da poligonal ( P
R
) é expressa
pela fração do erro de fechamento linear como
numerador e o perímetro total da poligonal ( P )
como numerador:
• O resultado deve ser dividido por 1/ P
R
para
expressar o erro de 1 m em toda a área levantada.

Ajustamento de poligonais
• Para qualquer poligonal fechada, o erro de
fechamento linear deve ser ajustado ou
distribuído para balancear a poligonal.
• O ajustamento deve ser realizado até mesmo se o
erro de fechamento for negligível ao representar a
poligonal em escala de mapa.

Ajustamento de poligonais
• Há vários métodos elementares disponíveis para
ajustar a poligonal, porém o mais comum é a regra
do compasso (método Bowditch).
• O ajustamento por mínimos quadrados é uma
técnica avançada que também pode ser utilizada.

Regra do compasso (Bowditch)
• No método do compasso, os valores de longitude
e de latitude são ajustados em relação a seu
comprimento.
• Embora esse método não seja tão rigoroso quanto
o método de mínimos quadrados, há uma
distribuição lógica dos erros de fechamento de
forma proporcional aos lados da poligonal
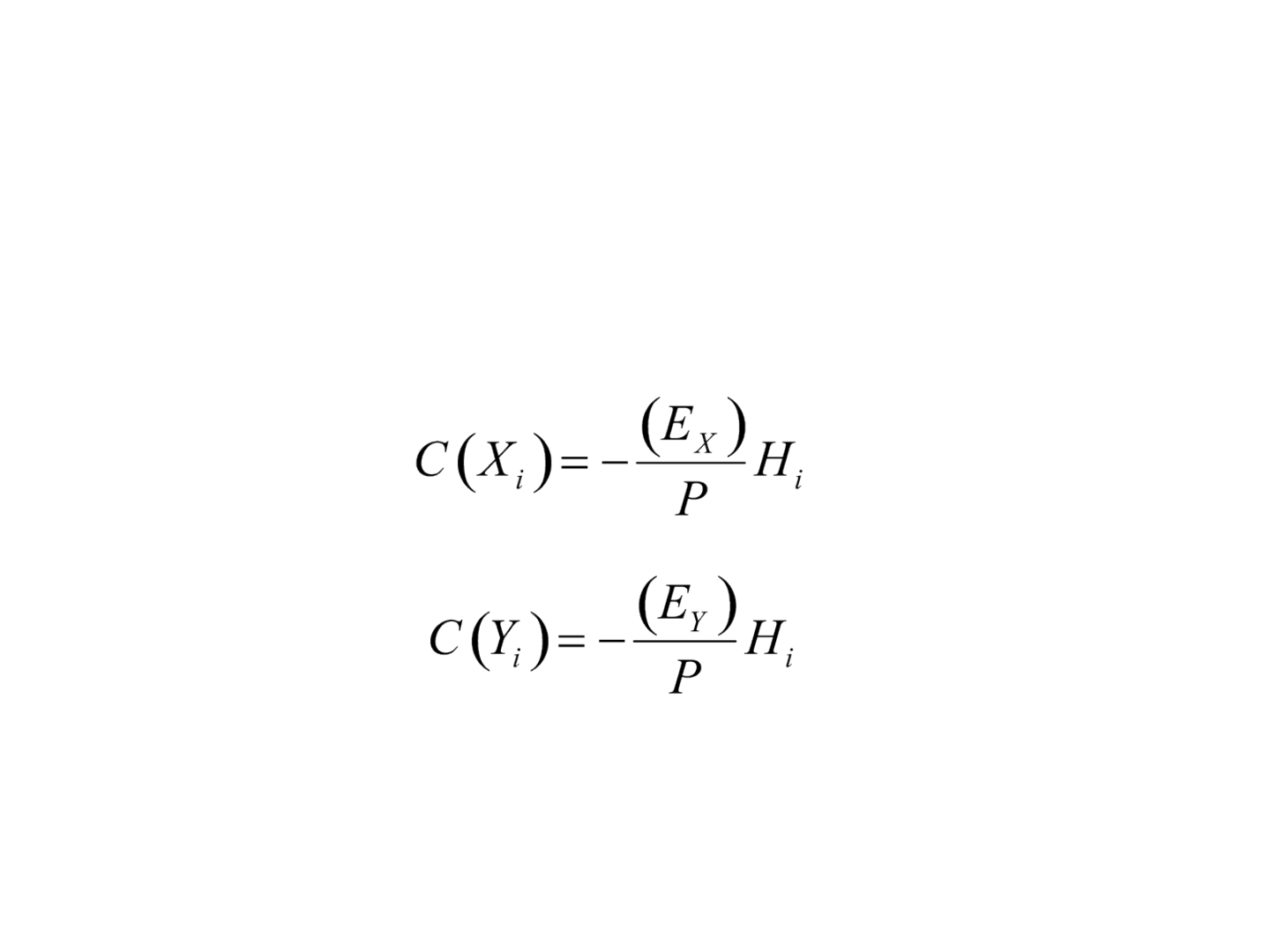
Regra do compasso (Bowditch)
• As correções de longitude, C( X
i
), e de latitude,
C(Y
i
), são realizadas conforme as seguintes regras:
em que H
i
é a distância horizontal do alinhamento a
ser corrigido.

Regra do compasso (Bowditch)
• Observar que o sinal de correção é oposto ao erro
de fechamento.
• As correções devem ser somadas algebricamente a
cada projeção.

Regra do compasso (Bowditch)
• Uma checagem pode ser realizada de modo que a
soma da coluna dos valores de longitude e de
latitude corrigidos deve ser igual a zero, podendo
ocorrer pequenas diferenças resultantes de
aproximações que devem ser eliminadas por meio
da revisão de uma das correções.

Cálculo final de comprimentos e
direções de poligonal
• Como os valores das linhas de longitude e de
latitude foram modificados no processo de
ajustamento, os valores de comprimento e
azimute também foram modificados.
• Com isso, é necessário calcular os comprimentos e
direções finais ou ajustados.

Cálculo final de comprimentos e
direções de poligonal
• Como as longitudes e as latitudes dos
alinhamentos corrigidos são conhecidos, o
comprimento e o azimute podem ser obtidos com
base nas relações do processo inverso
apresentadas na aula anterior sobre o método de
irradiação utilizando relações de arco tangente e
hipotenusa no triângulo retângulo.