
Medição indireta de distâncias
com instrumentos óticos
mecânicos
Prof. Dr. Marcelo de Carvalho Alves
Departamento de Engenharia
Universidade Federal de Lavras
Lavras, MG

Introdução
• Os medidores de distância indireta óticos e
mecânicos são denominados de taquímetros ou
taqueômetros.
• Nos medidores óticos e mecânicos o método
mais utilizado é o estadimétrico ou
taqueométrico.

Introdução
• Rapidez e exatidão são as grandes vantagens da
estadimetria em relação à medição direta de
distância.
• O método depende de treinamento do operador
e de auxiliares.
• Deve-se utilizar teodolito, nível, mira ou régua e
acessórios, como tripé.

• O termo taqueometria significa, do grego,
medições rápidas e o termo estádia é o plural da
palavra grega stadium.
• Relatos históricos indicam que o escocês James
Watt foi o desenvolvedor do método de
estadimetria, em 1771 .
Medição indireta com
instrumentos óticos mecânicos

• As observações de estádia foram obtidas por
visadas através da luneta com fios estadimétricos
de espaçamento conhecido no interior da luneta.
• O comprimento aparente interceptado no topo e
parte inferior da cruzeta é lido em uma haste
graduada, régua ou mira falante, posicionada na
vertical em relação ao ponto observado.
Medição indireta com
instrumentos óticos mecânicos

• A distância do telescópio até a régua é
determinada por relações de triângulos
semelhantes.
Medição indireta com
instrumentos óticos mecânicos
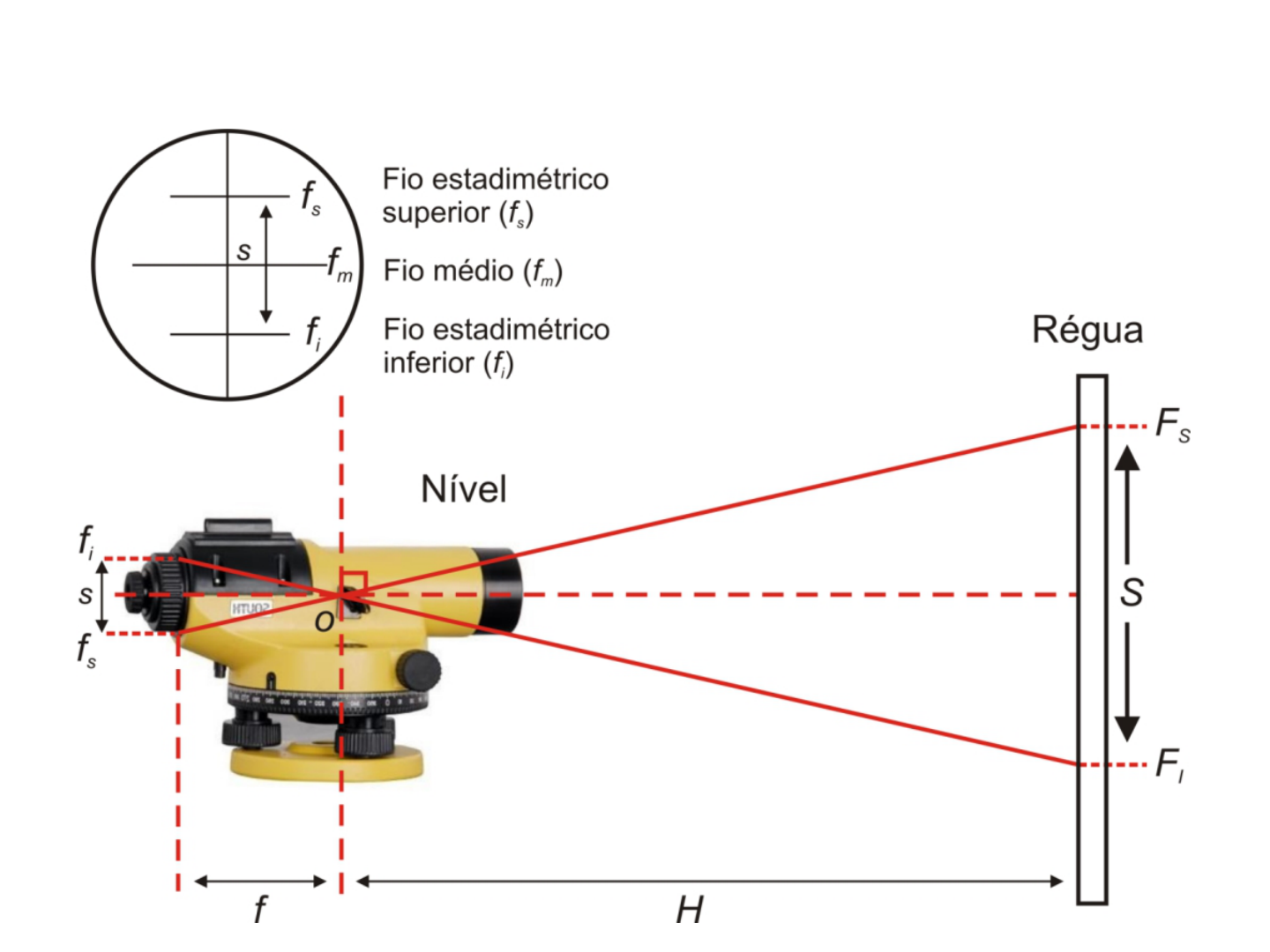
Medição indireta em terrenos planos

Medição indireta em terrenos planos
• A diferença entre as duas leituras dos fios
estadimétricos que interceptam a mira graduada
é chamada de número gerador.
• Os fios são espaçados de tal forma que a uma
distância de 30 m, 60 m e 80 m, a interseção em
uma mira vertical gera os números geradores de
0,3 m, 0,6 m e 0,8 m.

Medição indireta em terrenos planos
• Portanto, para se determinar uma distância
particular, a luneta é apontada sobre a mira e a
diferença entre o fio superior (F
S
) e inferior (F
I
) é
multiplicada por 100.
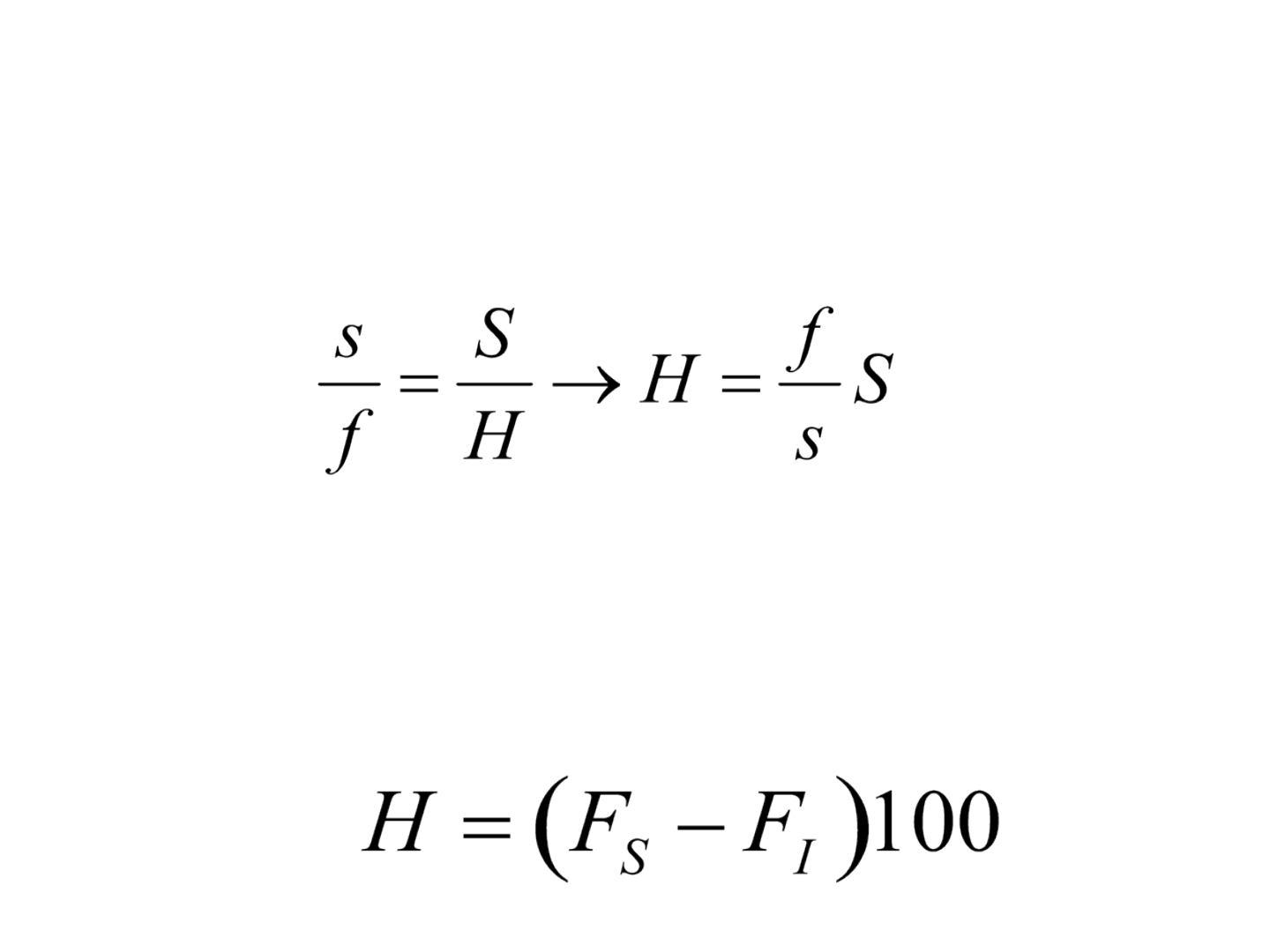
• Pela relação de triângulos semelhantes:
em que, f/s = 100 e S = (F
S
-F
I
).
• Portanto:
Medição indireta em terrenos planos

Medição indireta em terrenos
inclinados
• Ao trabalhar em terreno inclinado, o ângulo
vertical é utilizado para calcular a componente
horizontal da distância inclinada, bem como para
se determinar a diferença em altura entre dois
pontos.
• Nesse caso, a diferença entre os fios superior e
inferior na medição é inclinada (F
S
- F
I
)
i
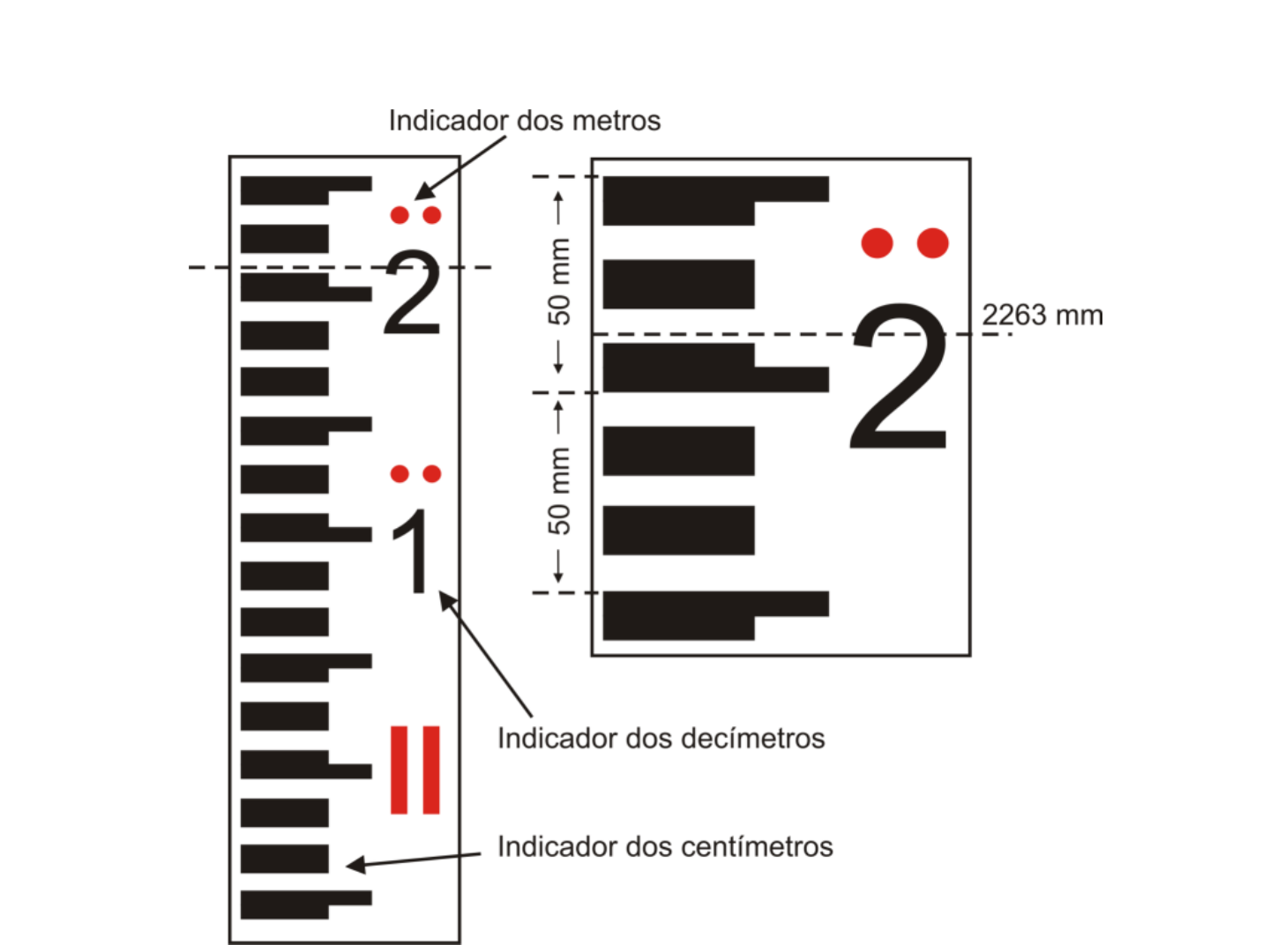
Leitura de régua
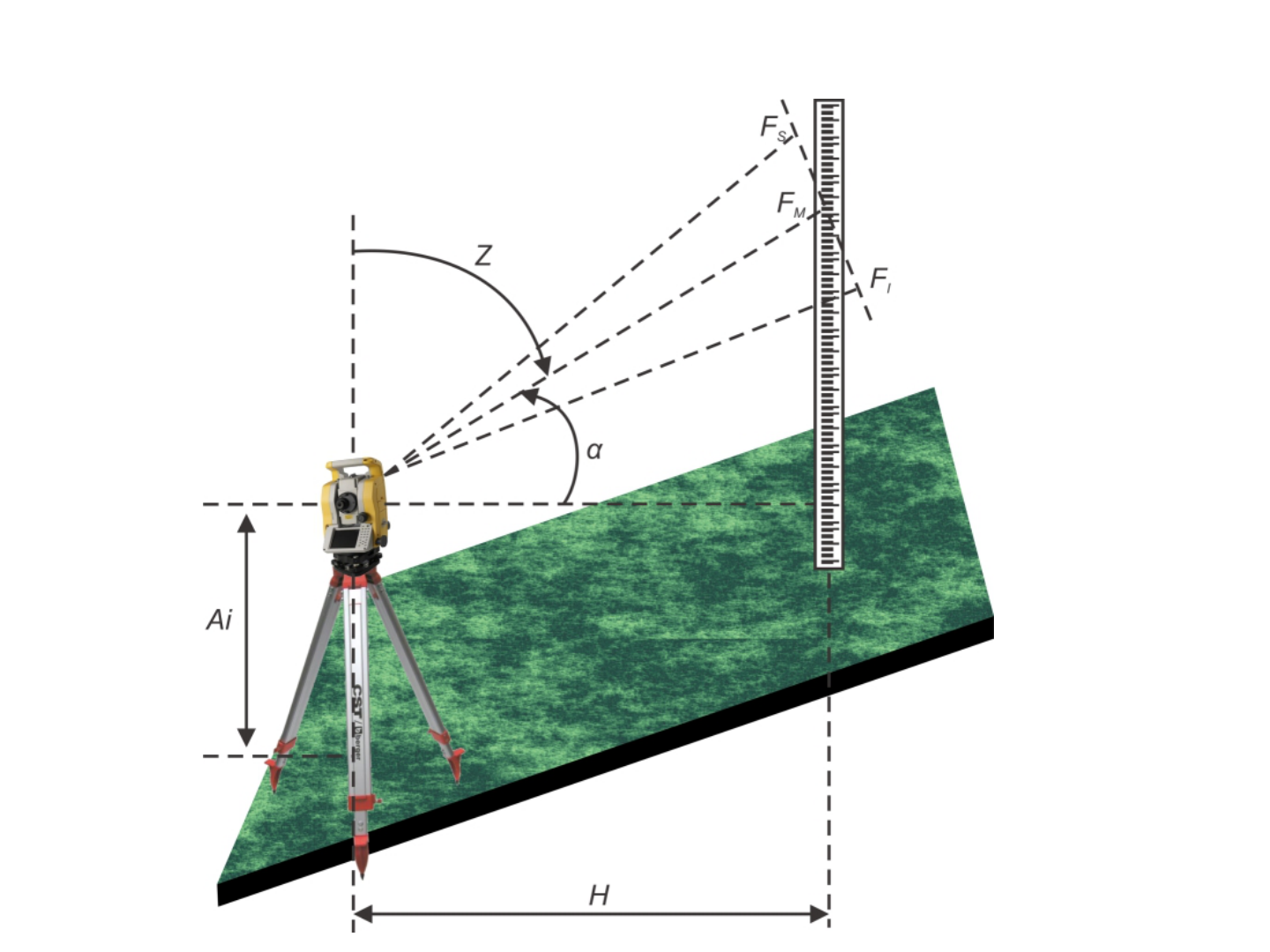
Medição indireta em terrenos
inclinados

• Fator de correção na leitura dos fios:
(F
S
- F
I
)
i
= (F
S
- F
I
) cosα
• Portanto:
L = (F
S
- F
I
)
i
100
Medição indireta em terrenos
inclinados

• Como:
H = Lcosα
• Então:
H = (F
S
- F
I
)
100 cos
2
α ; ou
H = (F
S
- F
I
)
100 sen
2
z
Medição indireta em terrenos
inclinados
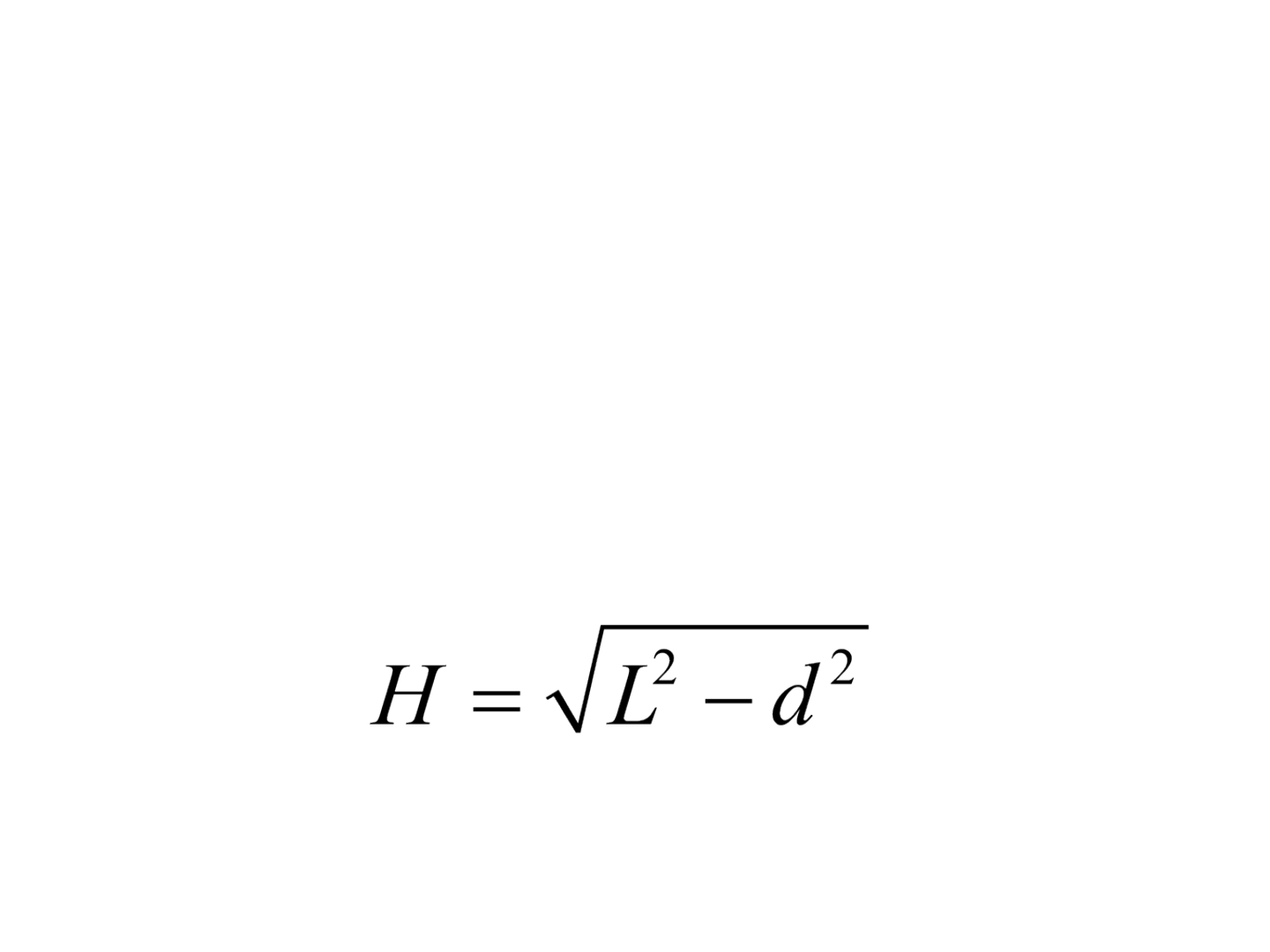
• De posse da diferença de nível entre dois pontos
e da distância inclinada, pode-se determinar a
distância horizontal por:
Determinação da diferença de
nível por estadimetria
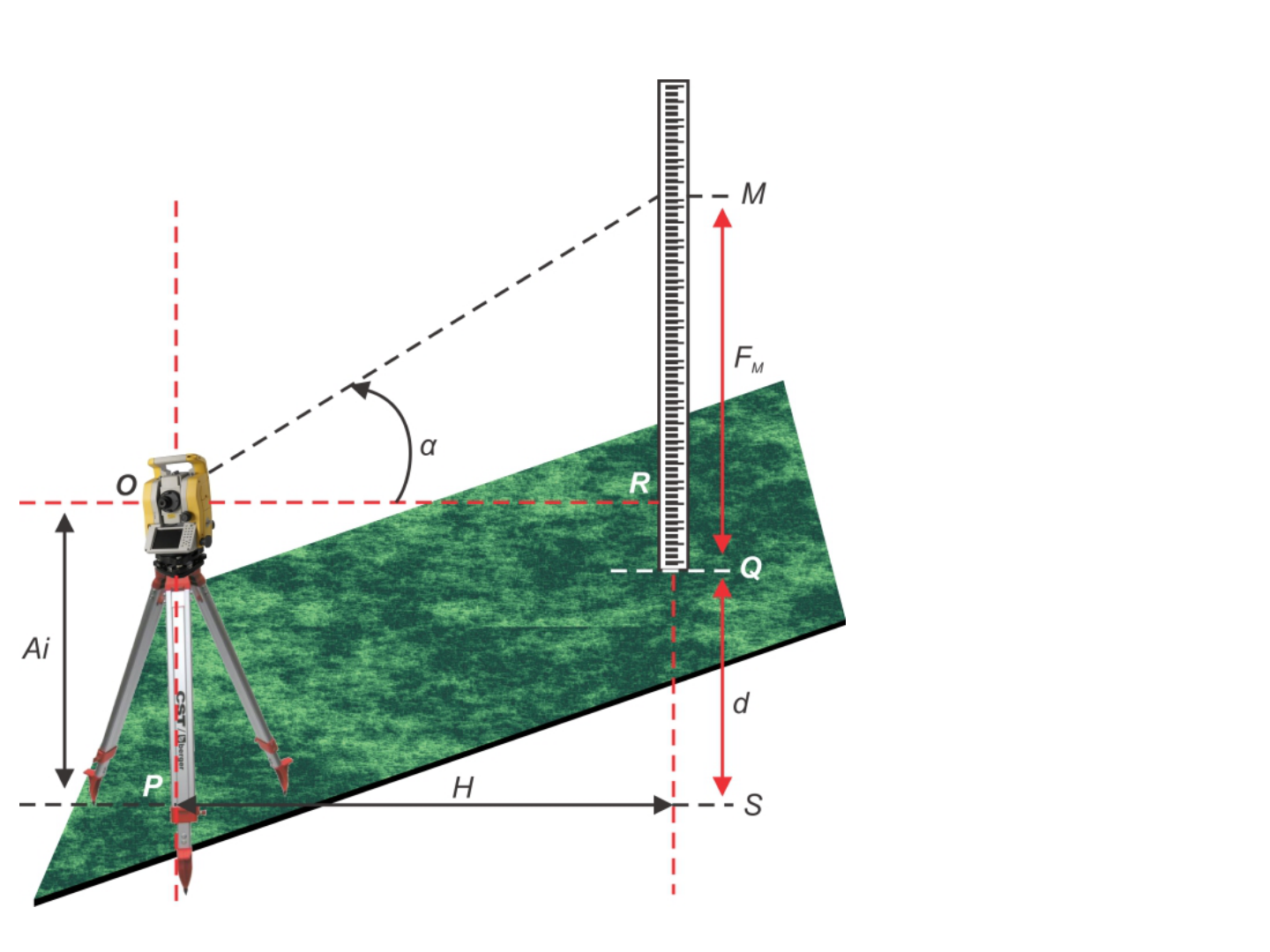
Determinação da diferença de nível por estadimetria
d = QS = RS + RM – MQ

• No triângulo ORM, RM = OR tg α
• Como OR = H, então: RM = H tg α
Determinação da diferença de
nível por estadimetria
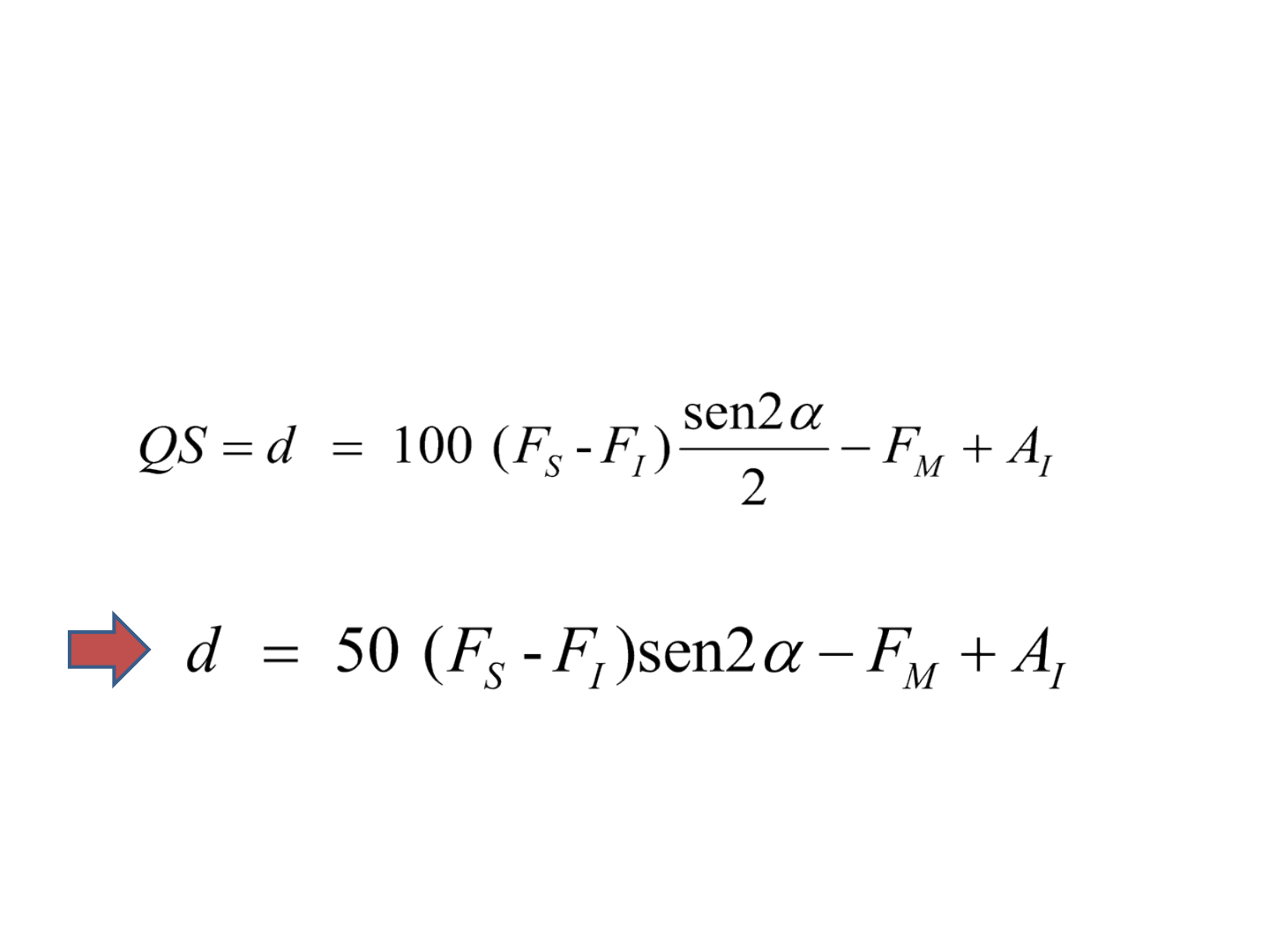
• Substituindo na primeira equação:
Determinação da diferença de
nível por estadimetria
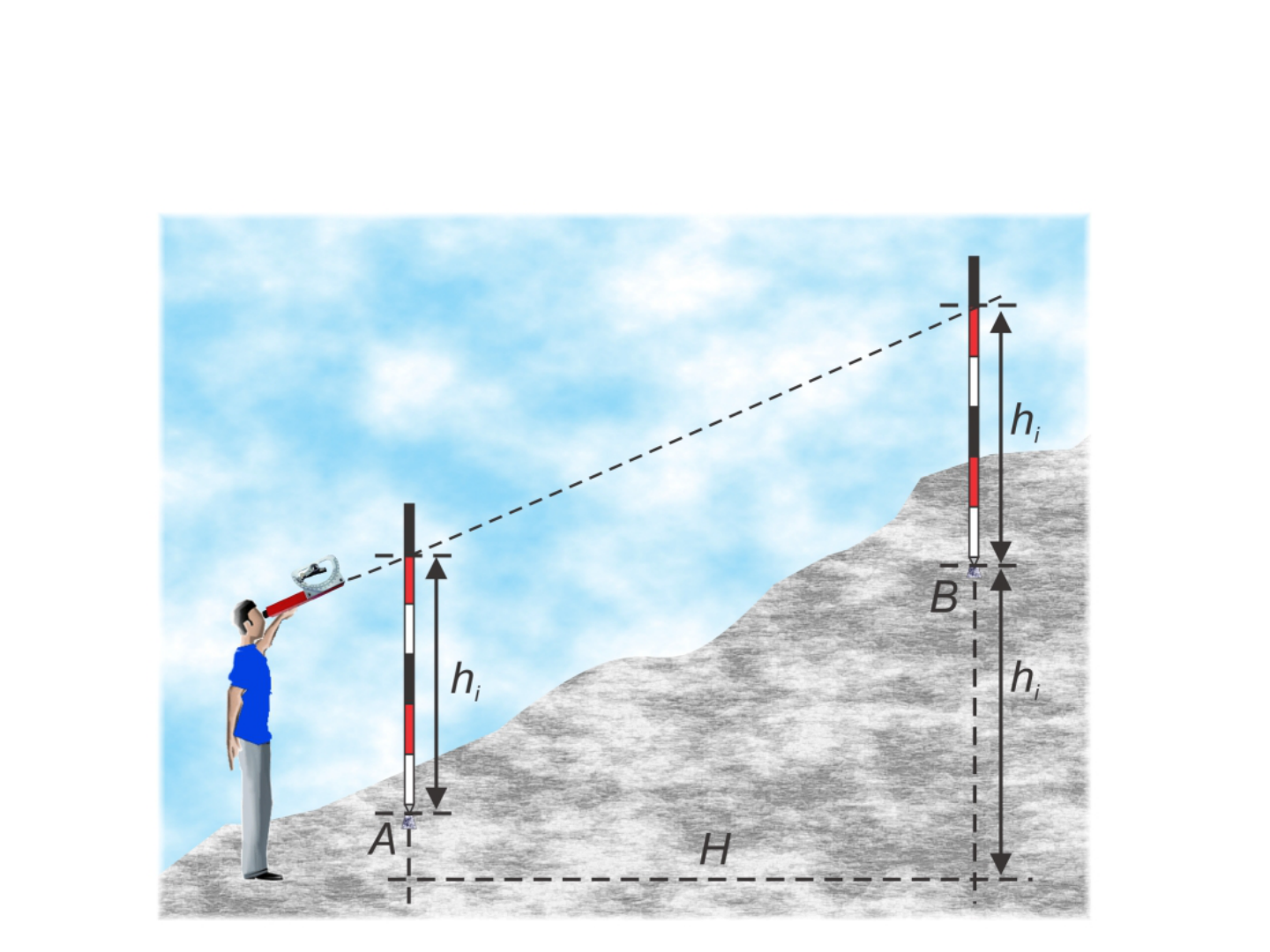
Determinação da diferença de
nível por trigronometria
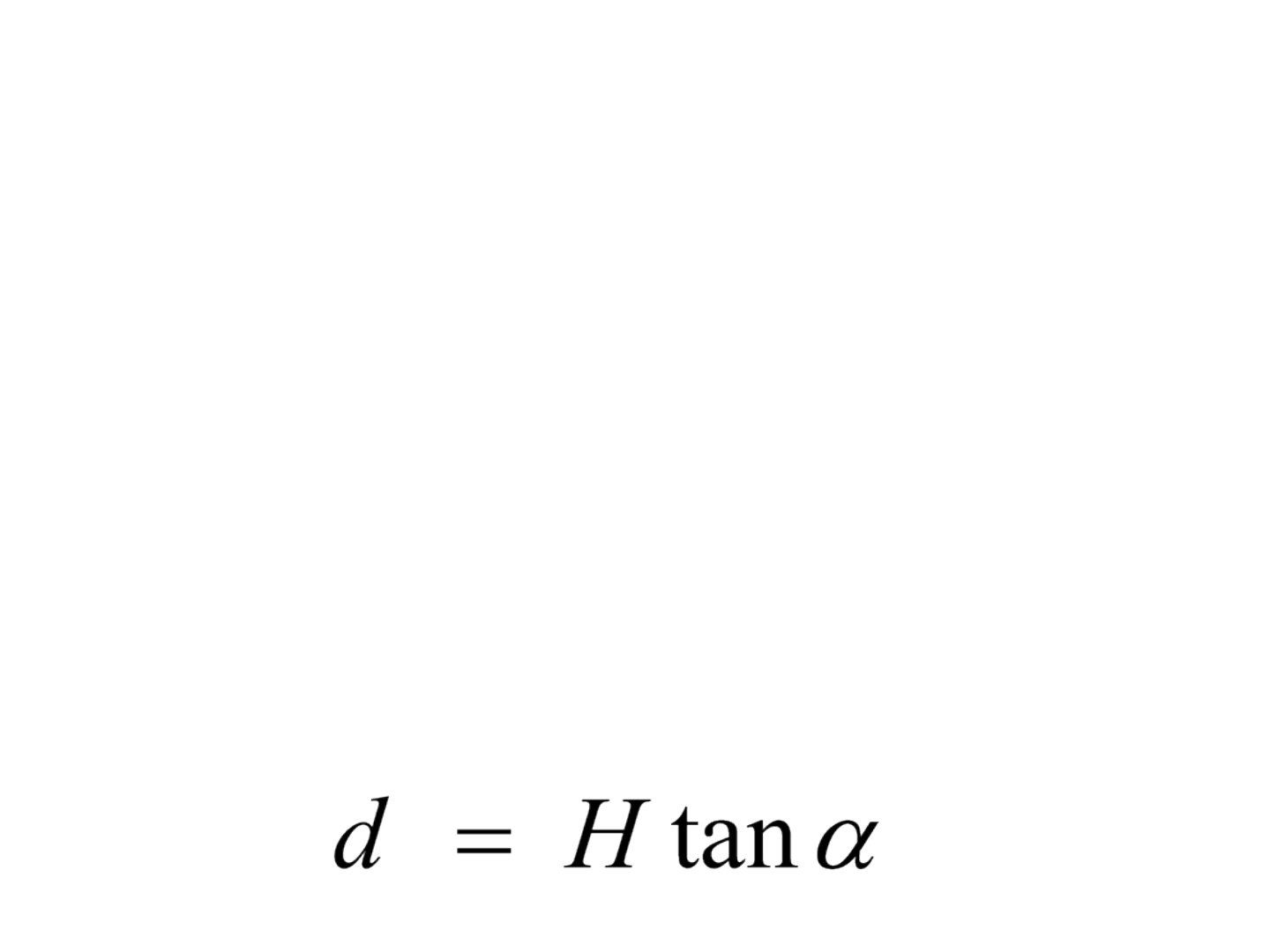
• Caso seja conhecida a distância horizontal ( H )
entre dois pontos A e B e o ângulo de inclinação
(α) entre o ponto de visada em A e um ponto de
mesma altura (h
i
) em B, a diferença de nível (d)
entre os dois pontos pode ser determinada por:
Determinação da diferença de
nível por trigronometria