
Medição direta de distâncias
Prof. Dr. Marcelo de Carvalho Alves
Departamento de Engenharia
Universidade Federal de Lavras
Lavras, MG

Introdução
• Na planimetria, o objetivo é obter grandezas
lineares e angulares num plano horizontal,
enquanto que na altimetria, são obtidas medidas
lineares e angulares na vertical e em planos que
contêm a vertical da localidade definida pela
direção do fio de prumo.

Introdução
• As grandezas lineares são principalmente a
distância horizontal ( H ), a distância vertical ou
diferença de nível (d). Quando se deseja medir a
distância inclinada AB ou de EF , é necessário
conhecer o ângulo de inclinação α .
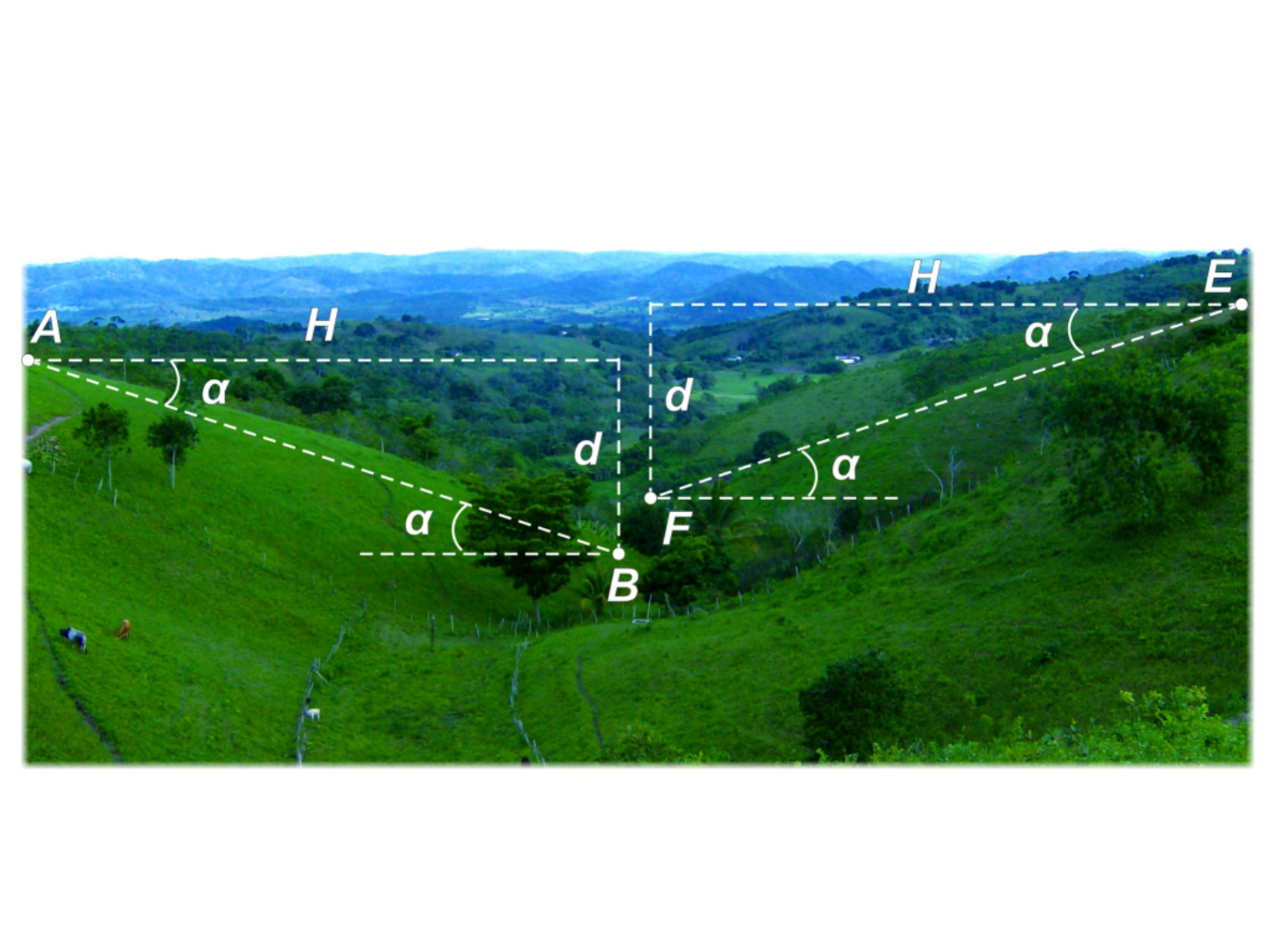
Medição de distância horizontal e diferença
de nível em levantamento topográfico

• Diastímetros: intrumentos utilizados na medição
direta de distâncias. Ex: Trenas, fitas de aço e
correntes de agrimensor
• Acessórios: Utilizados para localizar e materializar
o ponto topográfico no terreno. Ex: piquetes,
estacas, balizas e fichas.
Medição de distâncias com trena

Trenas, balizas e piquetes utilizados
no levantamento topográfico.

Medição de distâncias com trena
• Etapas: (i) esticar a trena sobre a superfície, (ii)
aplicar tensão nas extremidades, (iv) nivelar a
trena, (v) definir o comprimento a ser medido, (vi)
ler o valor demarcado e (vii) registrar a distância.
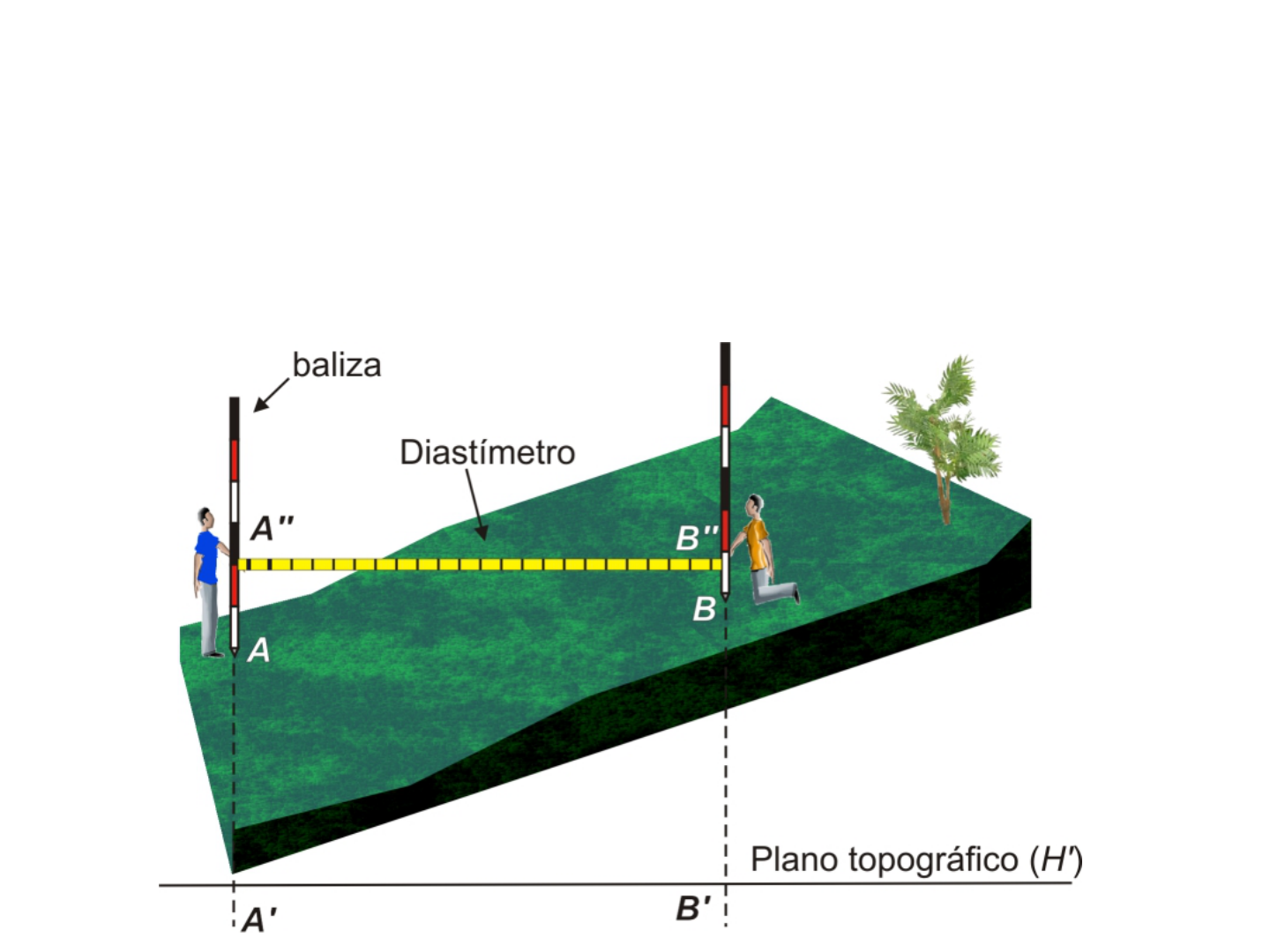
Medição de distâncias com trena
• Na medição de distância entre os pontos A e B ,
procura-se medir a projeção A’ , B’ no plano
topográfico H’

Medição de distâncias com trena
• Na medição de distâncias maiores que o
comprimento dos diastímetros, deve-se evitar
sair do alinhamento, com o uso de balizamentos.
• No balizamento, precisa-se de três pessoas, o
balizeiro de ré, o de vante e o intermediário, cada
um com uma baliza
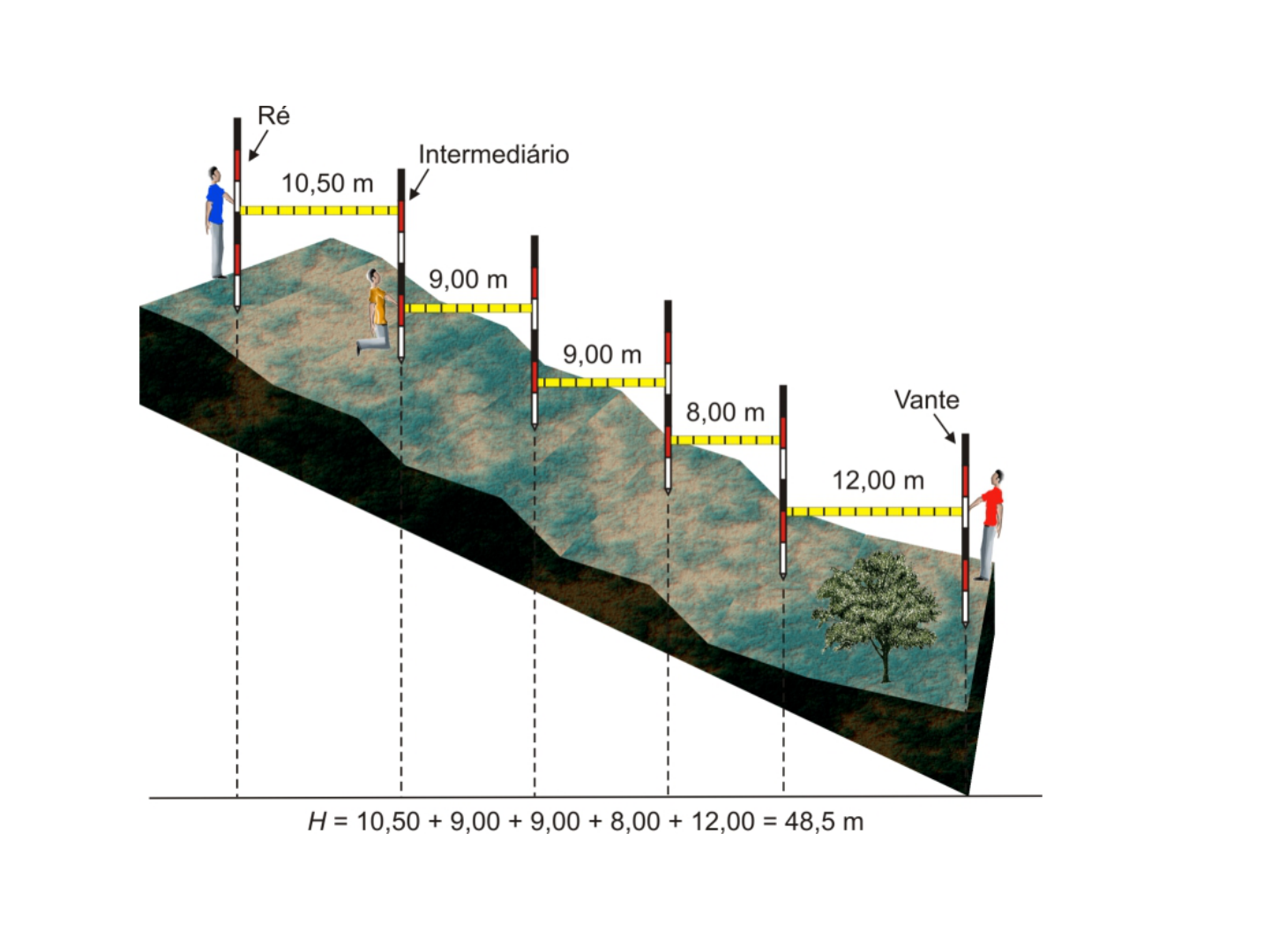
Balizamento
Medição de grandes distâncias com diastímetro

Medição com trena em terrenos
inclinados ou sobre vegetação
• A trena pode ser mantida horizontalmente com
fios de prumo.
• A trena pode ser mantida sobre a inclinação, e
uma correção pode ser realizada para se obter a
distância horizontal.
• O ângulo vertical pode ser medido para cada
inclinação, para o cálculo posterior da distância
horizontal.
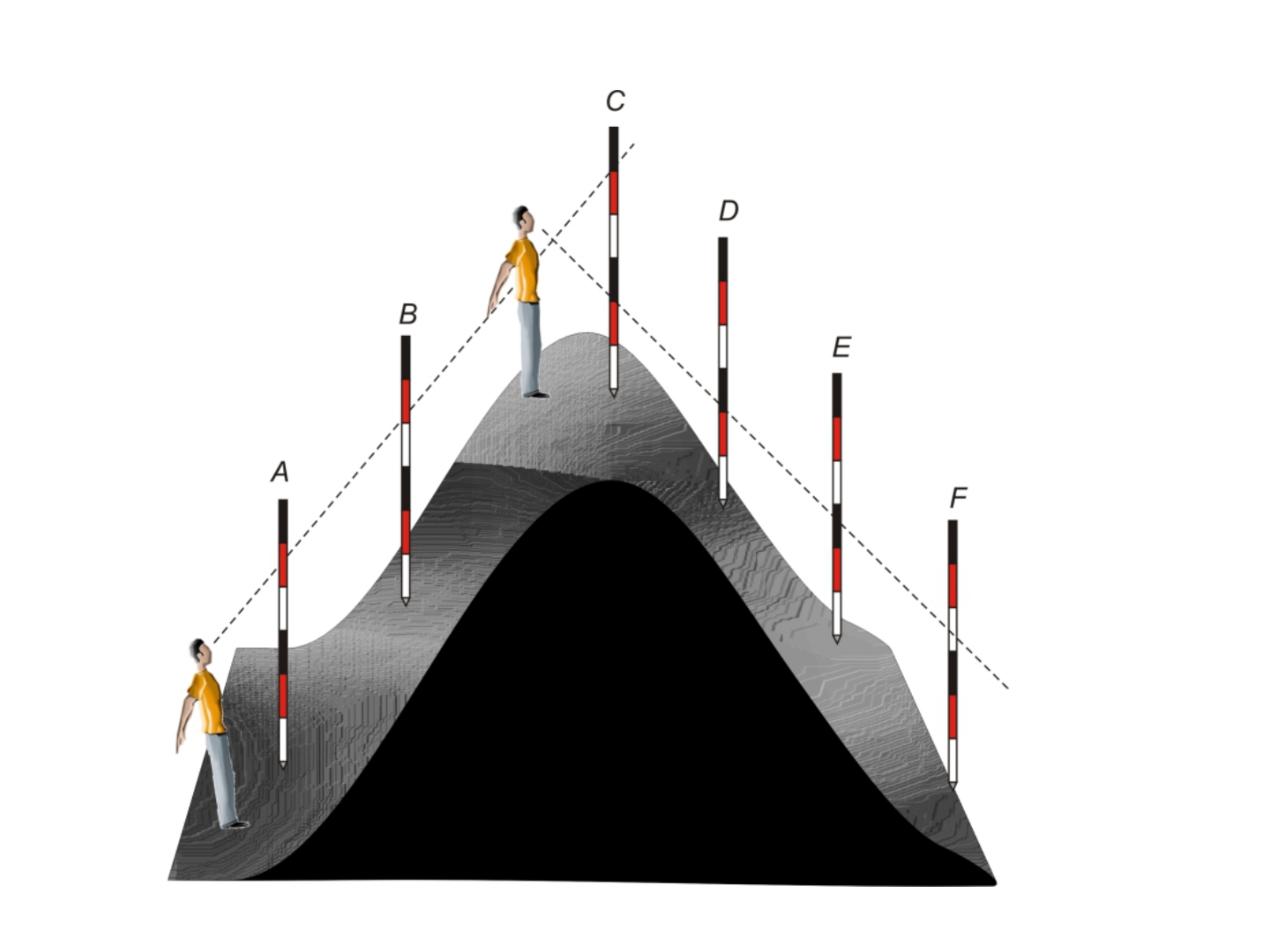
Prolongamento de um alinhamento
Prolongamento de alinhamento de grandes distâncias por meio de balizas
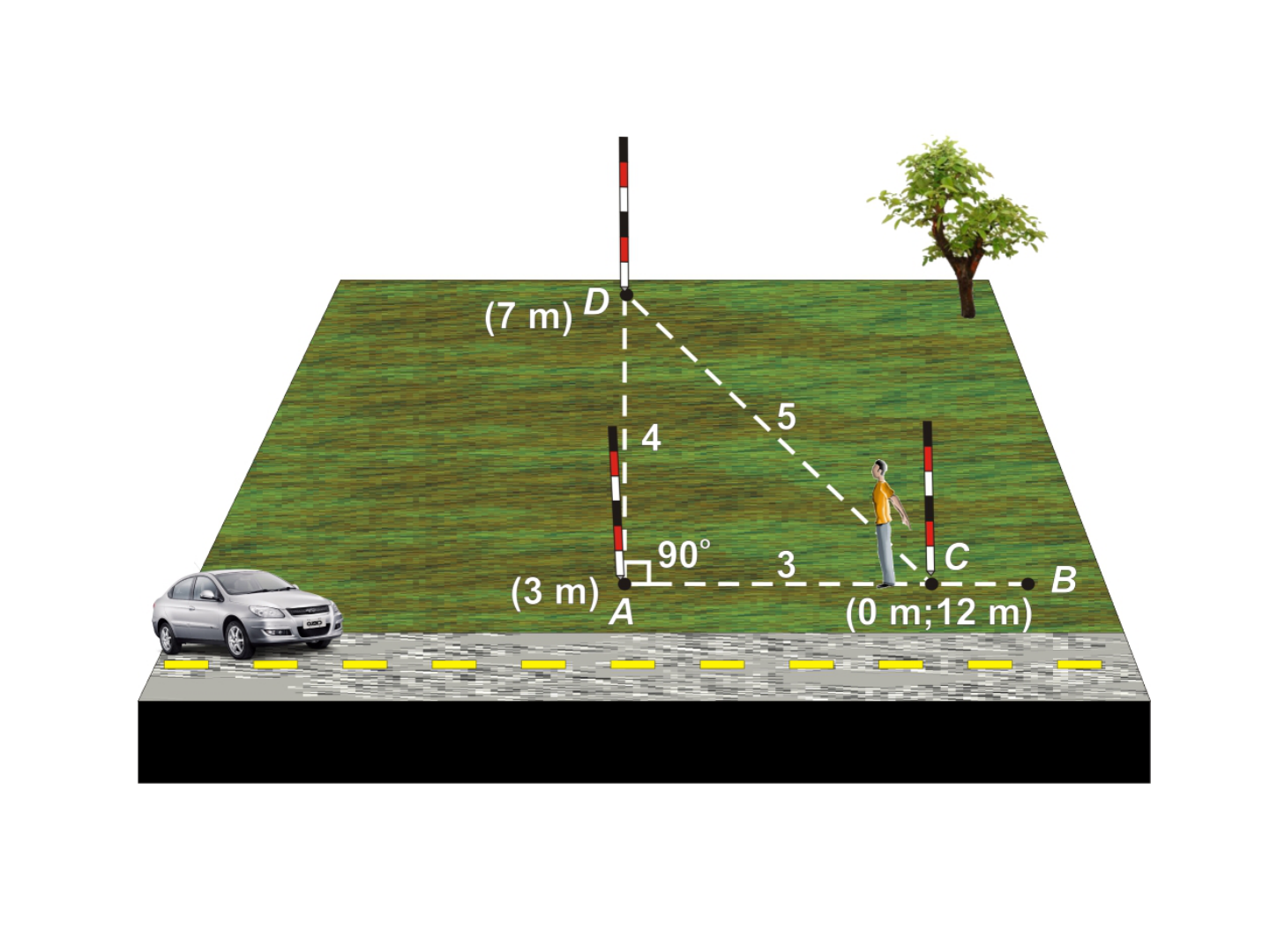
Traçado de perpendiculares
• Uso do triângulo retângulo para traçar
perpendiculares
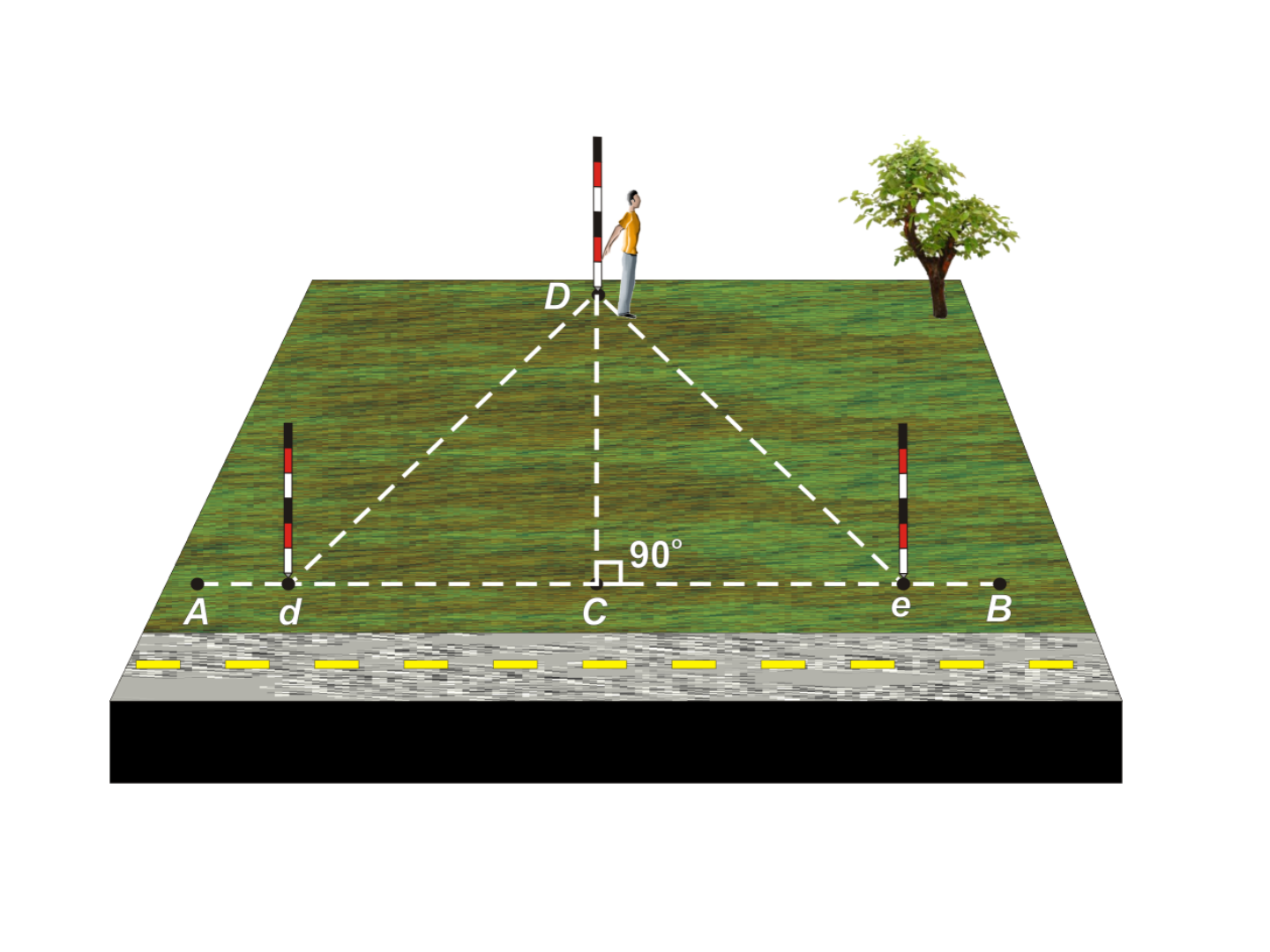
Traçado de perpendiculares
• Uso do triângulo isósceles para traçar
perpendiculares
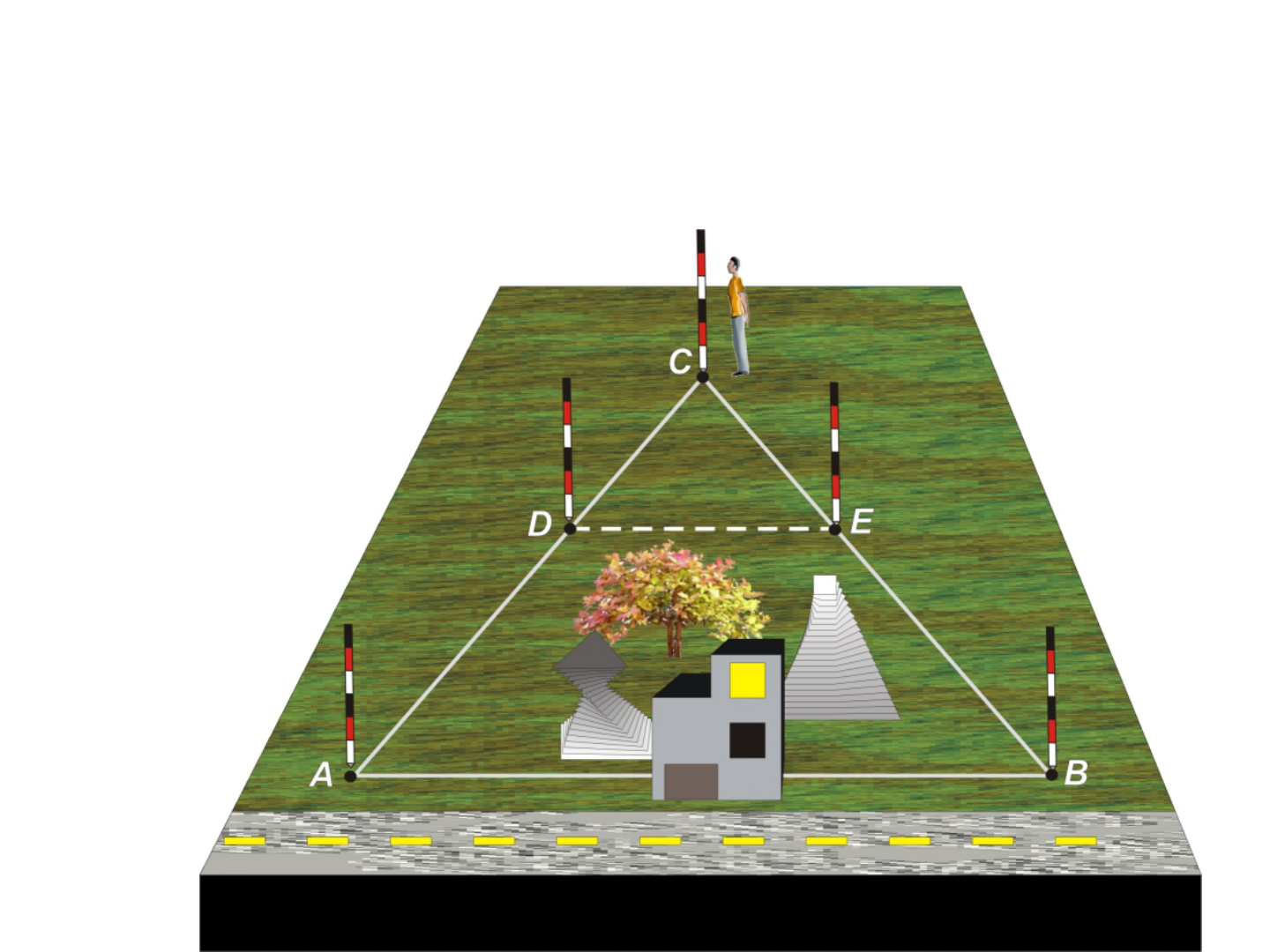
Transposição de obstáculos
• Pontos extremos do alinhamento não
intervisíveis
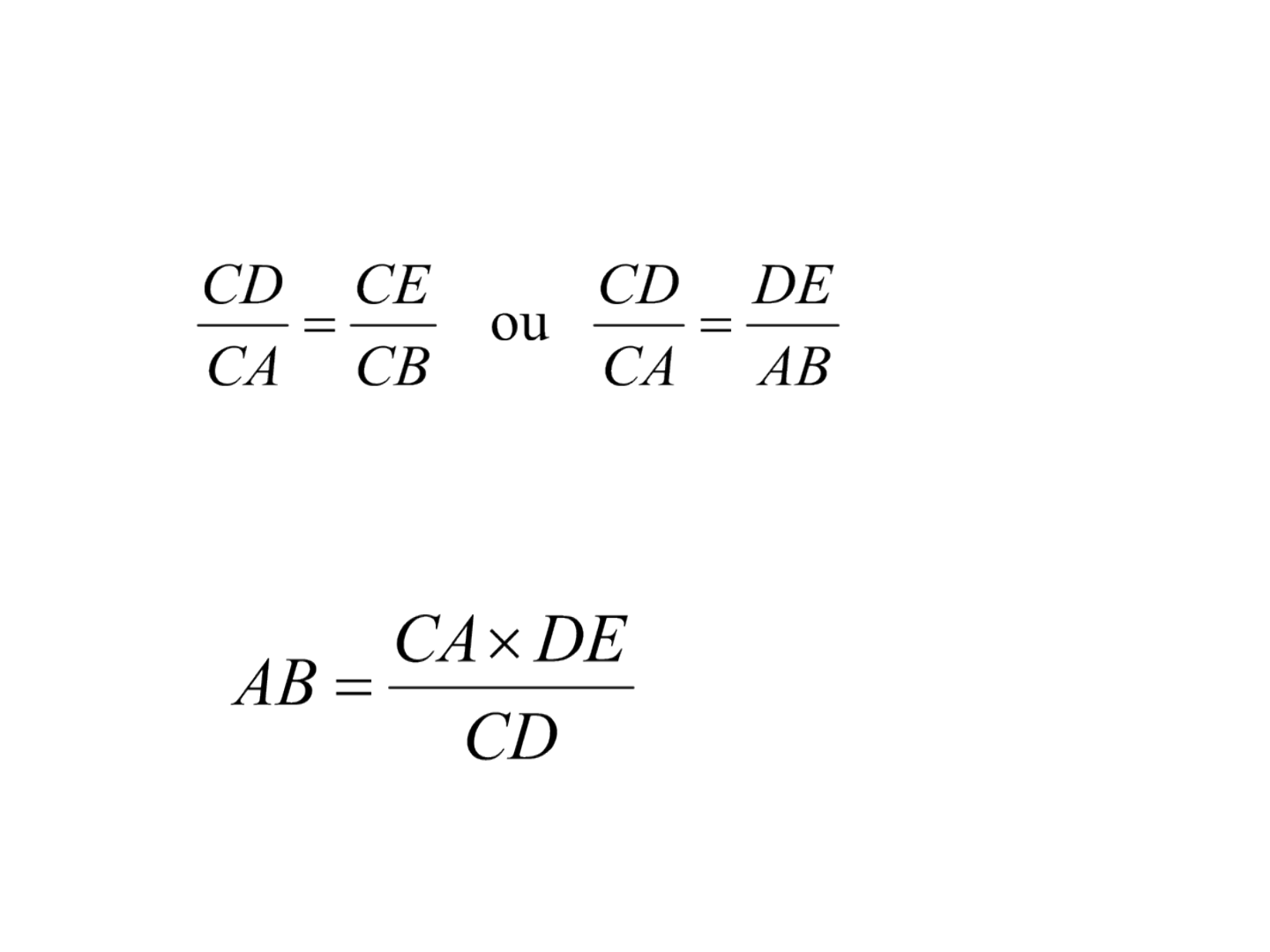
Transposição de obstáculos
• Para os triângulos formados tem-se:
em que,
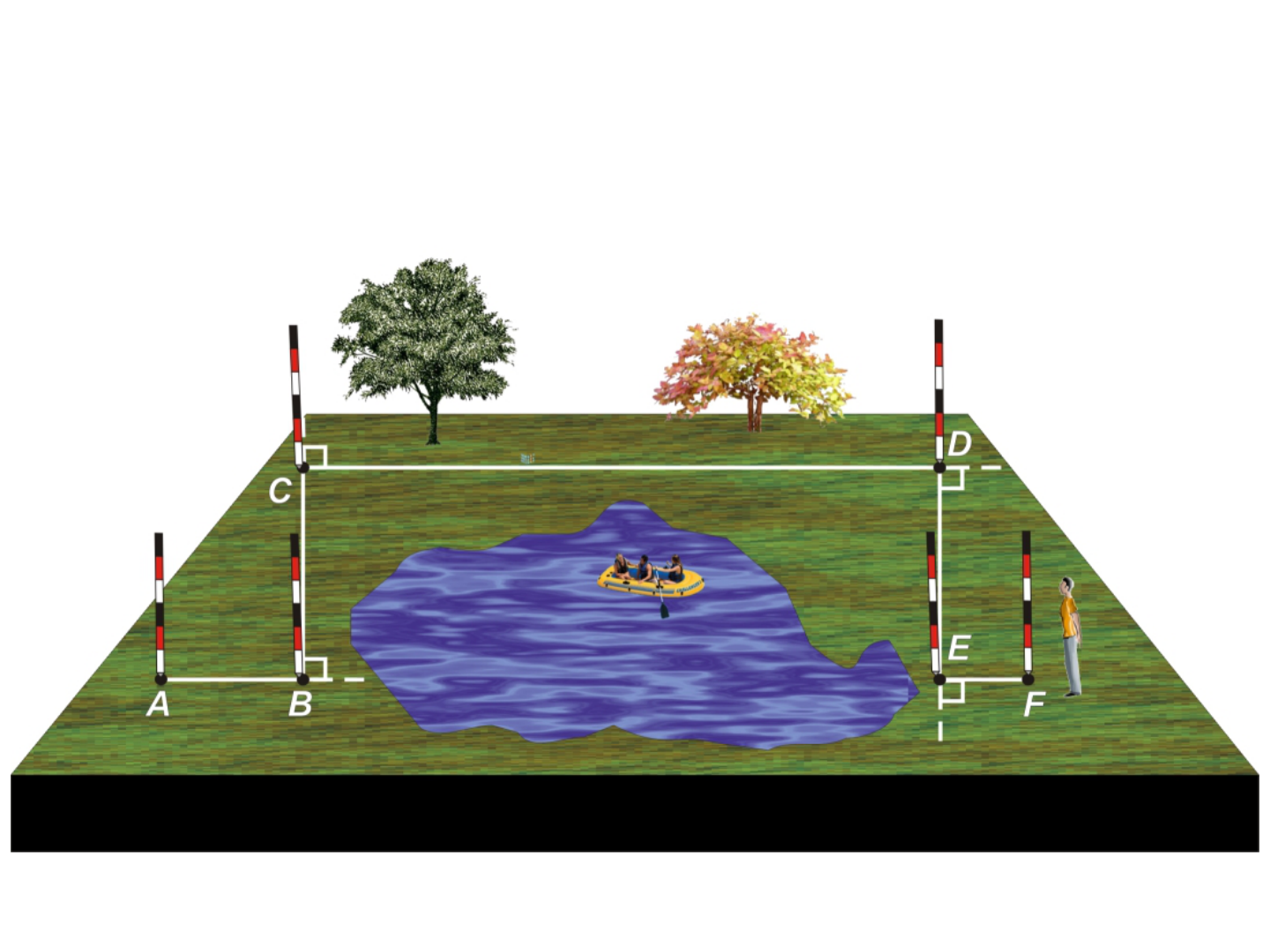
Transposição de obstáculos
• Pontos extremos do alinhamento visíveis
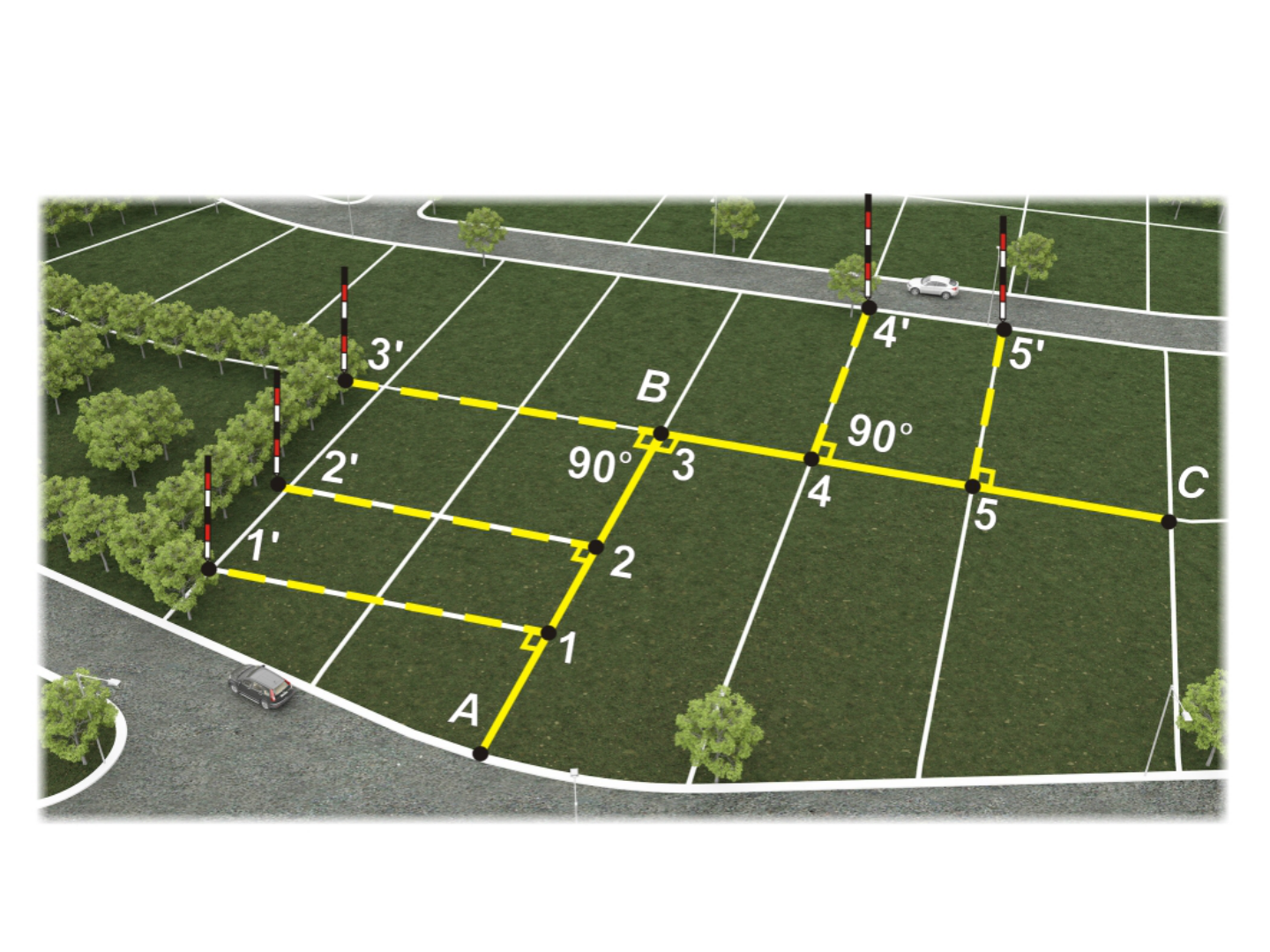
Localização de detalhes
Localização de detalhes com o uso de diastímetros.
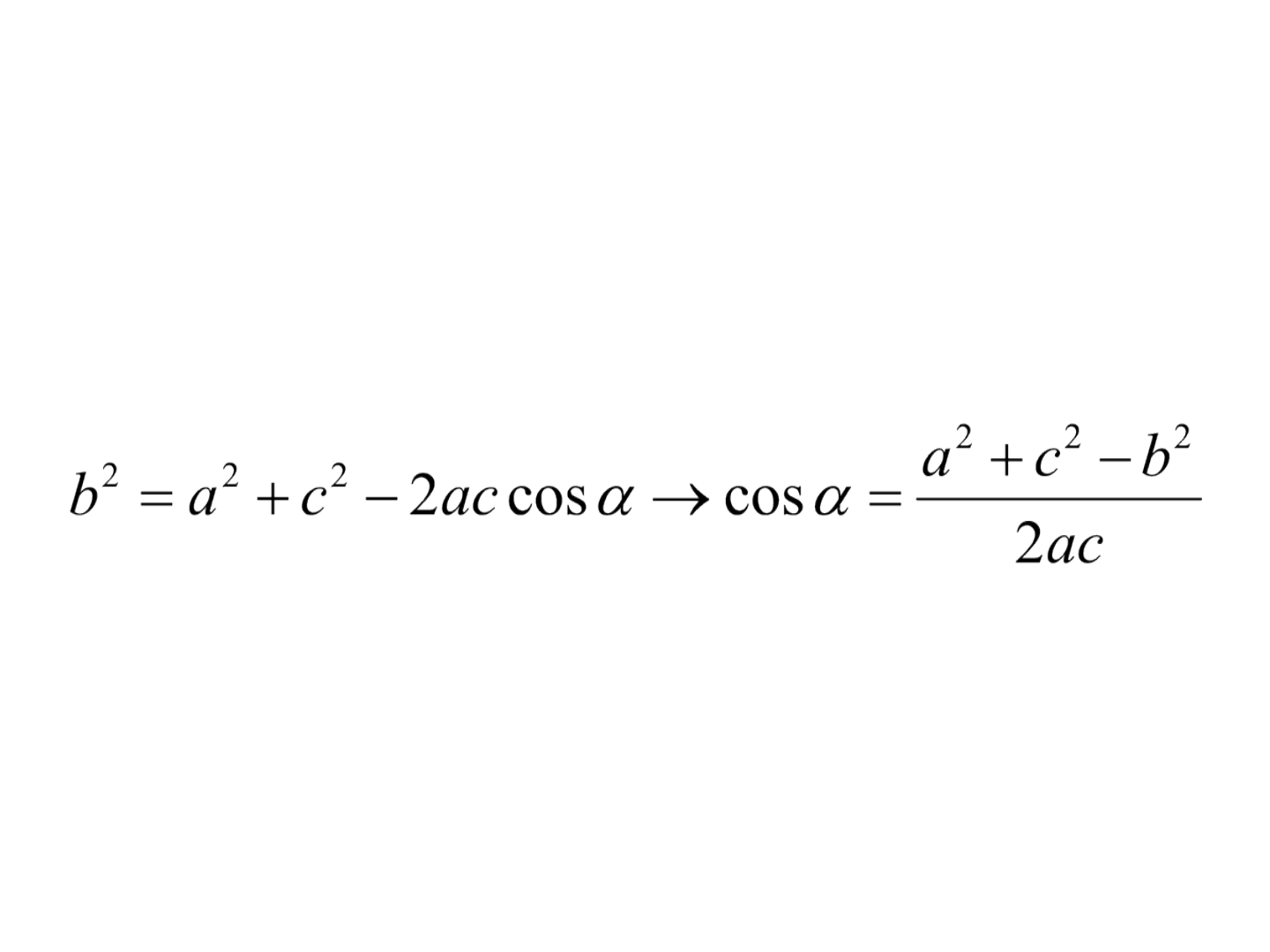
Medição de ângulos e levantamento
planimétrico com diastímetros
• lei dos co-senos
• Na prática, pode-se utilizar a = c , para que o
ângulo possa ser determinado por tabelas.

Caderneta de campo para
levantamento de uma poligonal com
diastímetro
Alinhamento H (m) Corda (m)
A – B 4
B – C 3
A – C 5
C – D 4
D – E 3
C – E 5
E – F 3
F – G 4
G – E 5*
G – H 4
H – A 3
A – G 5
*Corda de ângulo externo.
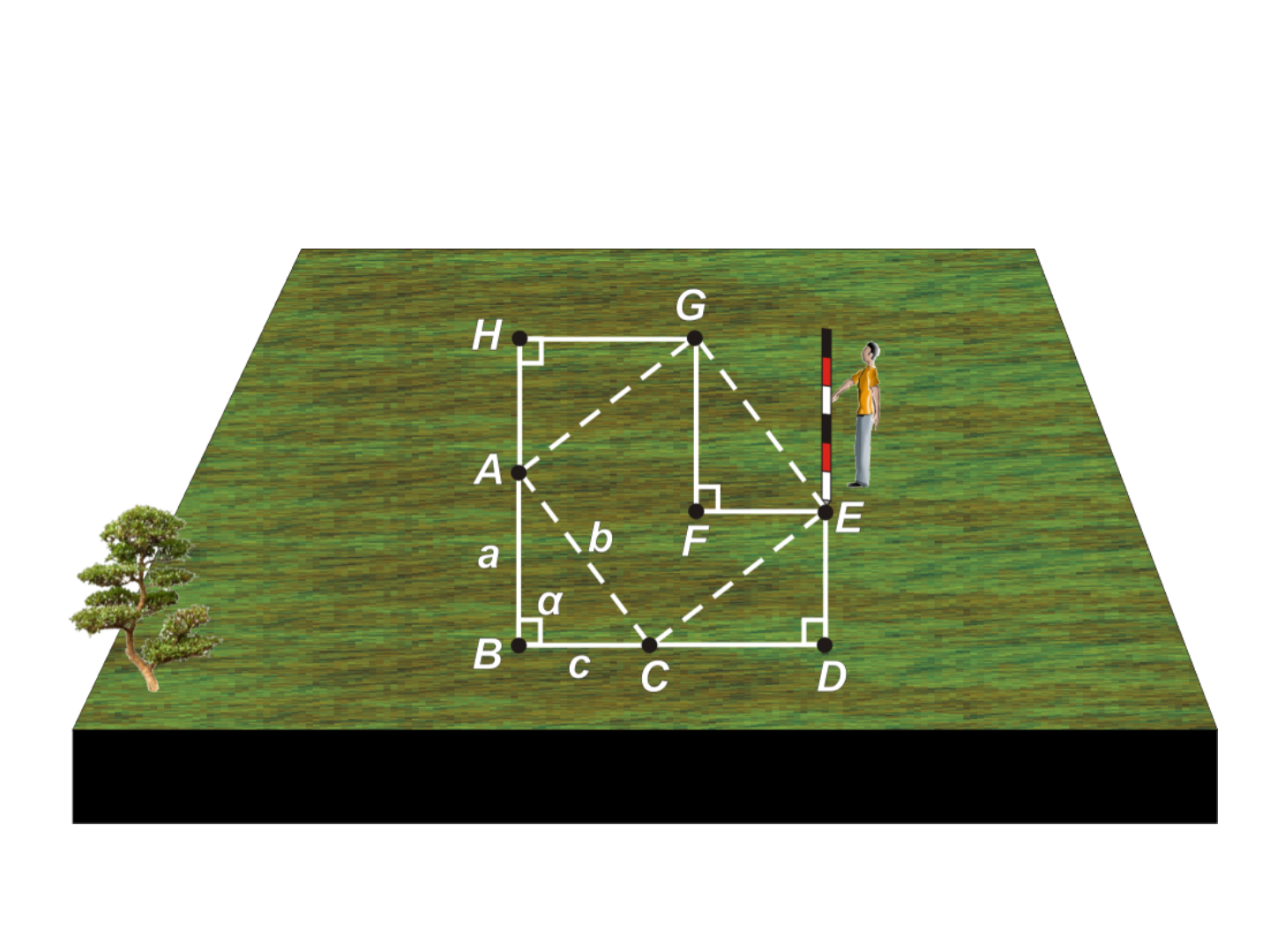
Levantamento da poligonal
ABCDEFGH com diastímetro

Avaliação da área
• A área ( A ) pode ser determinada observando o
gráfico da poligonal e calculando-se a área do
triângulo BAC da Figura anterior com base nas
seguintes equações:
ou
em que,
a,b, c são os lados do triângulo.
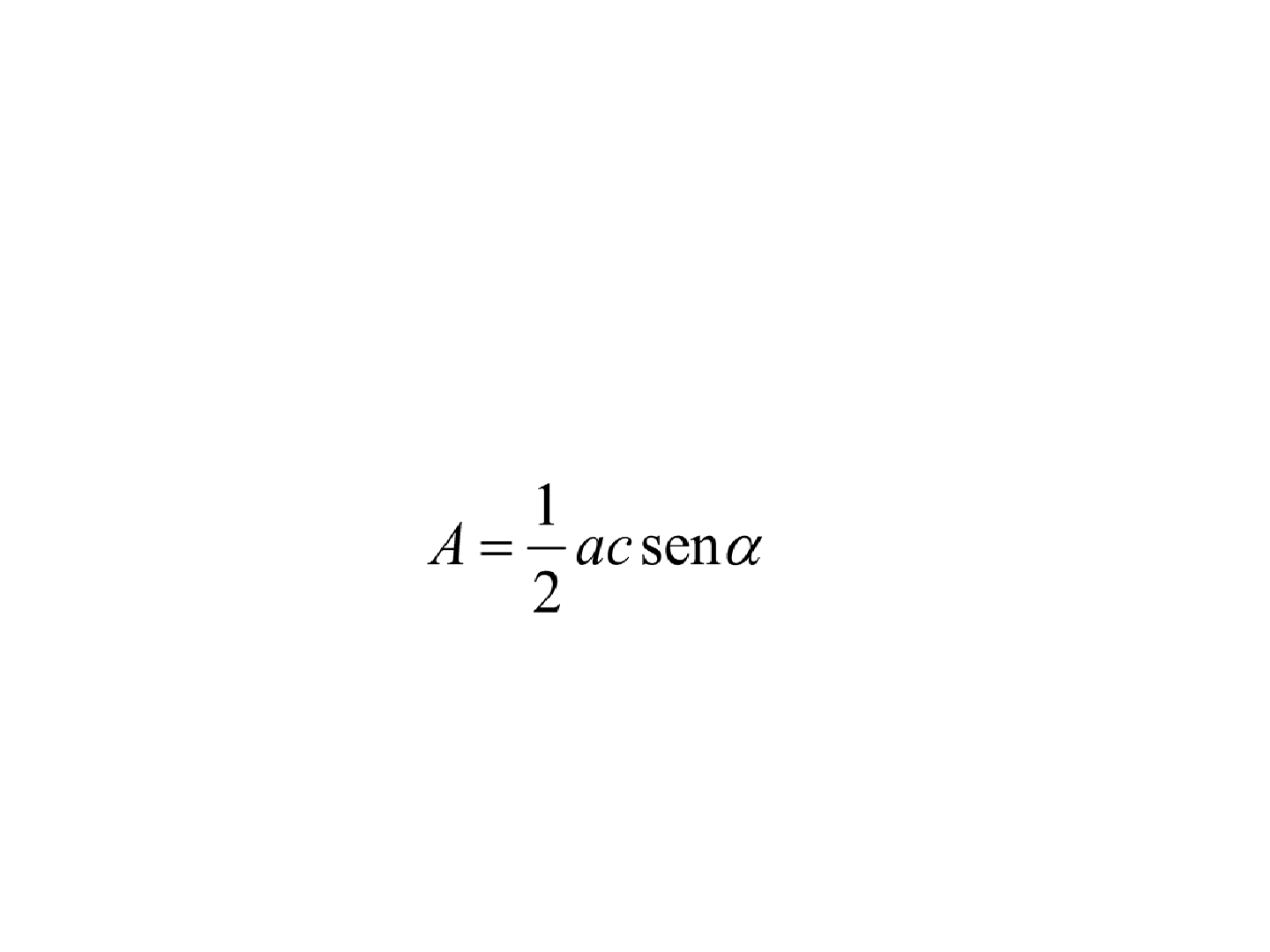
Avaliação da área
• No caso de se conhecer o valor de um ângulo, a
área do triângulo BAC da Figura anterior pode ser
calculada por:

Correções de distâncias medidas
com trena
• As cinco principais situações nas quais o topógrafo
pode necessitar aplicar correções durante a medição
ou locação com trena são:
• Calibração de trenas.
• Variações de temperatura.
• Inclinações.
• Catenária.
• Tensão incorreta.

Correções de distâncias medidas
com trena
• Após determinar o erro, a distância real para uma
linha medida pode ser obtida incorporando as
correções na seguinte equação:
• Distância real = Distância medida + ∑ correções

Calibração de trenas
• Levantamento
já
já
realizado
realizado: Mediu-se a distância e
posteriormente constatou-se tamanho equivocado da
trena, pode-se adotar a regra: para uma
trena
trena
mais
mais
longa
longa deve-se
adicionar
adicionar uma correção de distância e
para uma
trena
trena
mais
mais
curta
curta deve-se
subtrair
subtrair o valor
de correção.

Calibração de trenas
•
Planejamento
Planejamento
do levantamento: Pretende-se
realizar uma medição com uma trena mais longa ou
mais curta: para uma
trena
trena
mais
mais
longa
longa deve-se
subtrair
subtrair uma correção de distância e para uma
trena
trena
mais curta
mais curta deve-se
somar
somar o valor de correção.
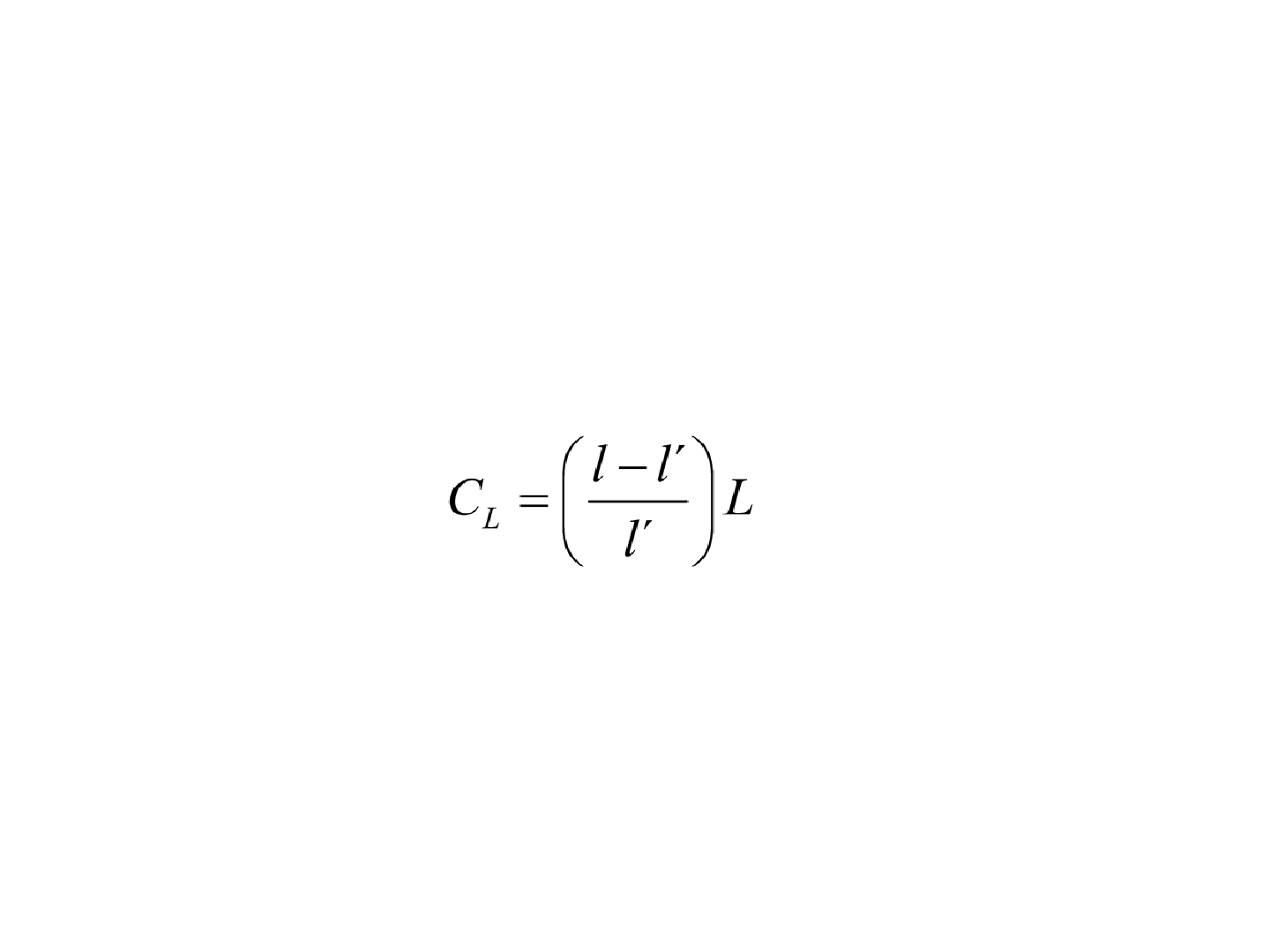
Calibração de trenas
• A correção erro causado pelo comprimento incorreto
da trena pode ser:
• em que C
L
é
a correção (m), l é a medida real da
trena (m), l´ é o comprimento nominal da trena (m) e L
é a medida registrada do comprimento da linha (m).

Variações de temperatura
• O coeficiente de dilatação linear das trenas de aço
é 0,0000116 por grau Celsius.
• A mudança de temperatura de 5º C causará uma
mudança no comprimento de aproximadamente
0,002 m em uma trena de 30 m.

Variações de temperatura
• A correção de uma trena para variações de
temperatura (C
t
) é :
C
t
= k(T
1
- T) L
• em que, k é o coeficiente termal de expansão e
contração da trena, T
1
é a temperatura (
o
C) no
momento da medição, T
é a temperatura da
trena (
o
C) sob condições padrão e L é o
comprimento da linha (m).

Correções de inclinação e de alinhamento
horizontal
• Se o ângulo de altura ( α ) é determinado, a
distância horizontal entre os pontos A e B pode
ser calculada por meio da relação:
H = Lcos α
• em que H é a distância horizontal (m) entre os
pontos, L é o comprimento da declividade (m)
entre os pontos e α, o ângulo de altura (
o
) a partir
do plano horizontal, normalmente obtido por
clinômetro ou teodolito.
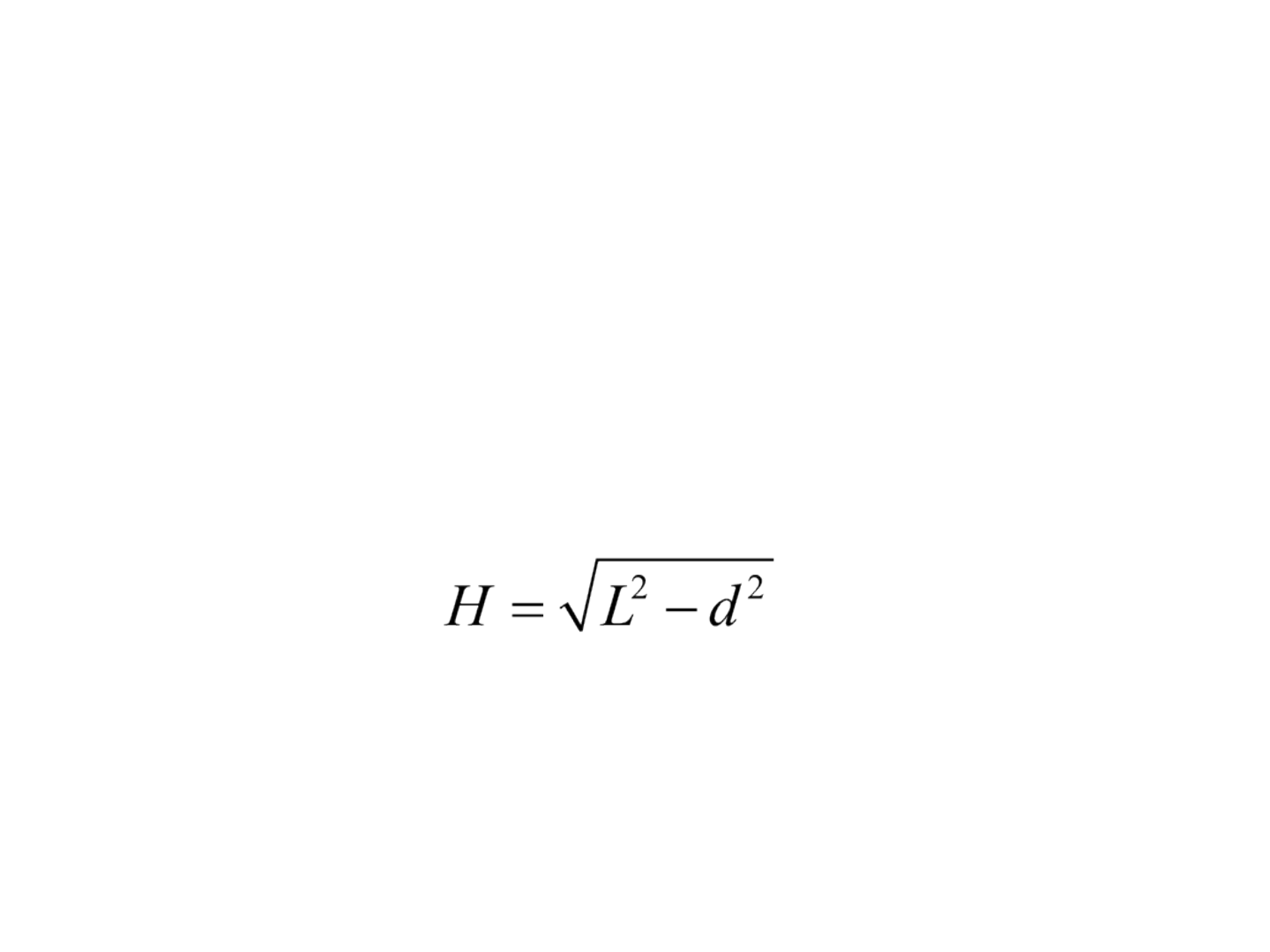
Correções de inclinação e de alinhamento
horizontal
• Se a diferença de elevação d entre os dois pontos
é conhecida, a distância horizontal pode ser
calculada pelo teorema de Pitágoras:
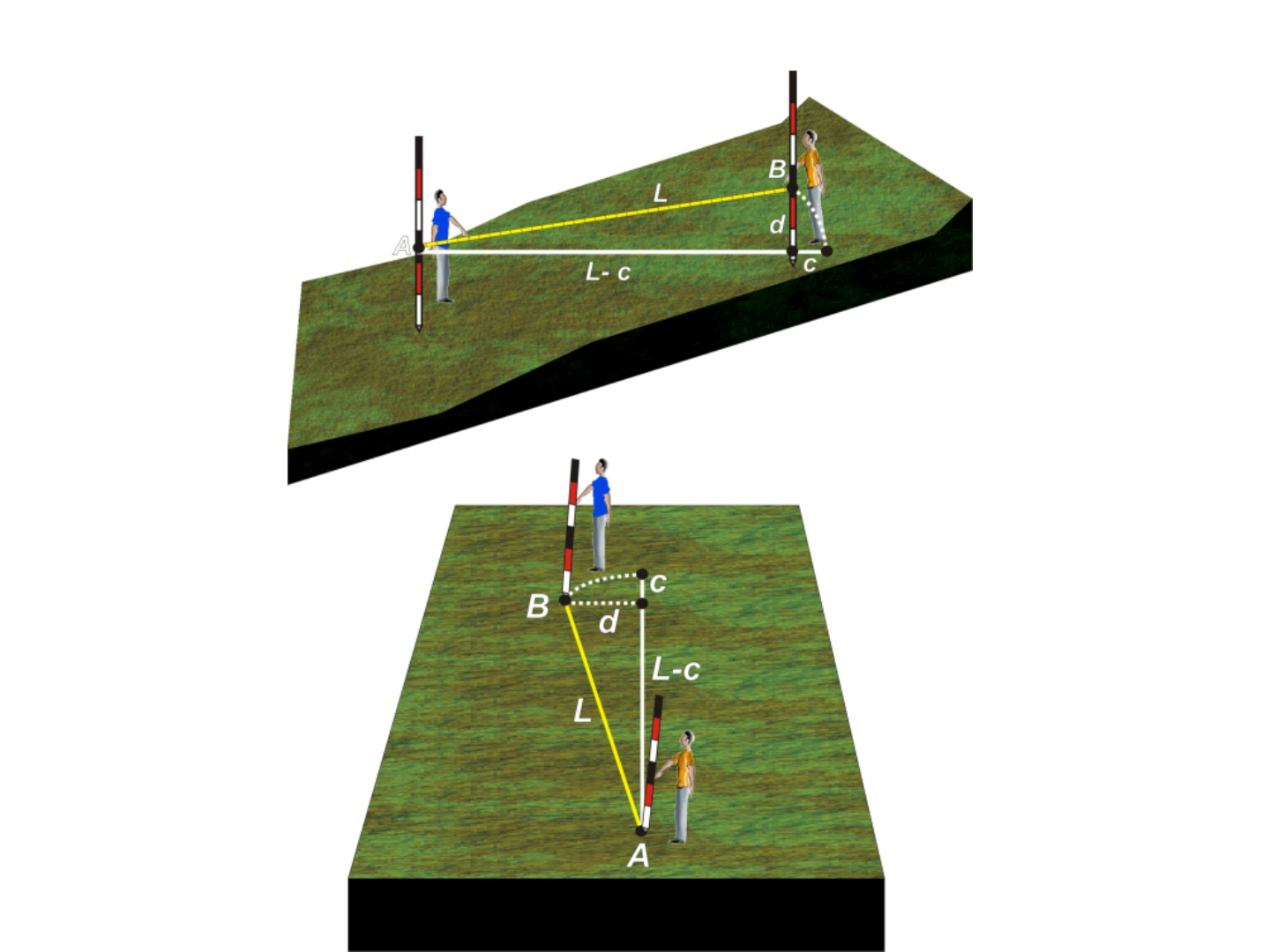
Correções de inclinação e de alinhamento horizontal
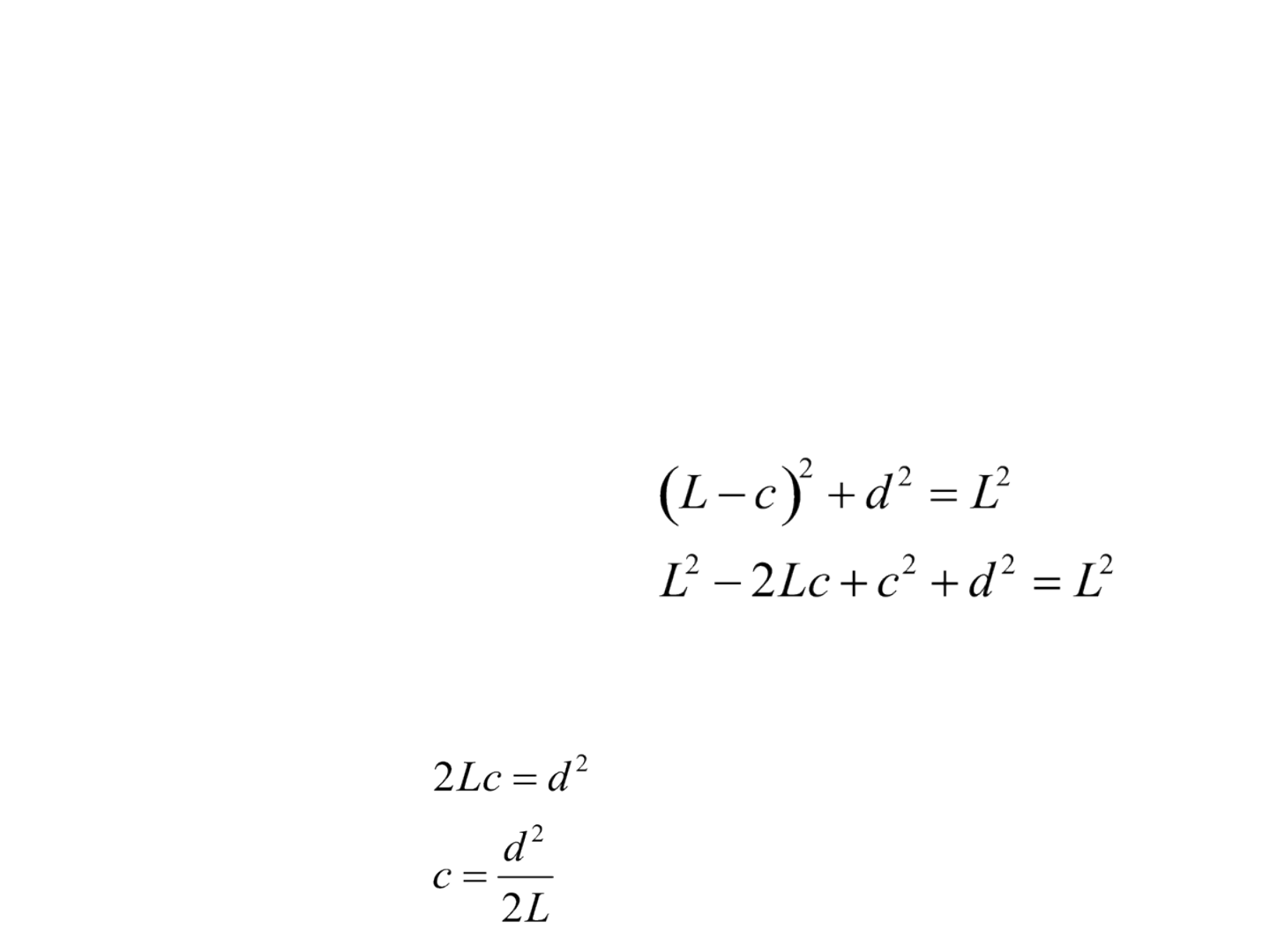
Correções de inclinação e de alinhamento
horizontal
• Considere c o fator de correção causado pelo erro
de alinhamento horizontal ou inclinação e L-c a
distância horizontal H:
• Na prática, o termo c
2
pode ser desprezado,
portanto:

Correções de tensão
• Quando uma trena é esticada com uma tensão
maior do que a padrão, a extensão da trena será
maior do que o comprimento padrão.
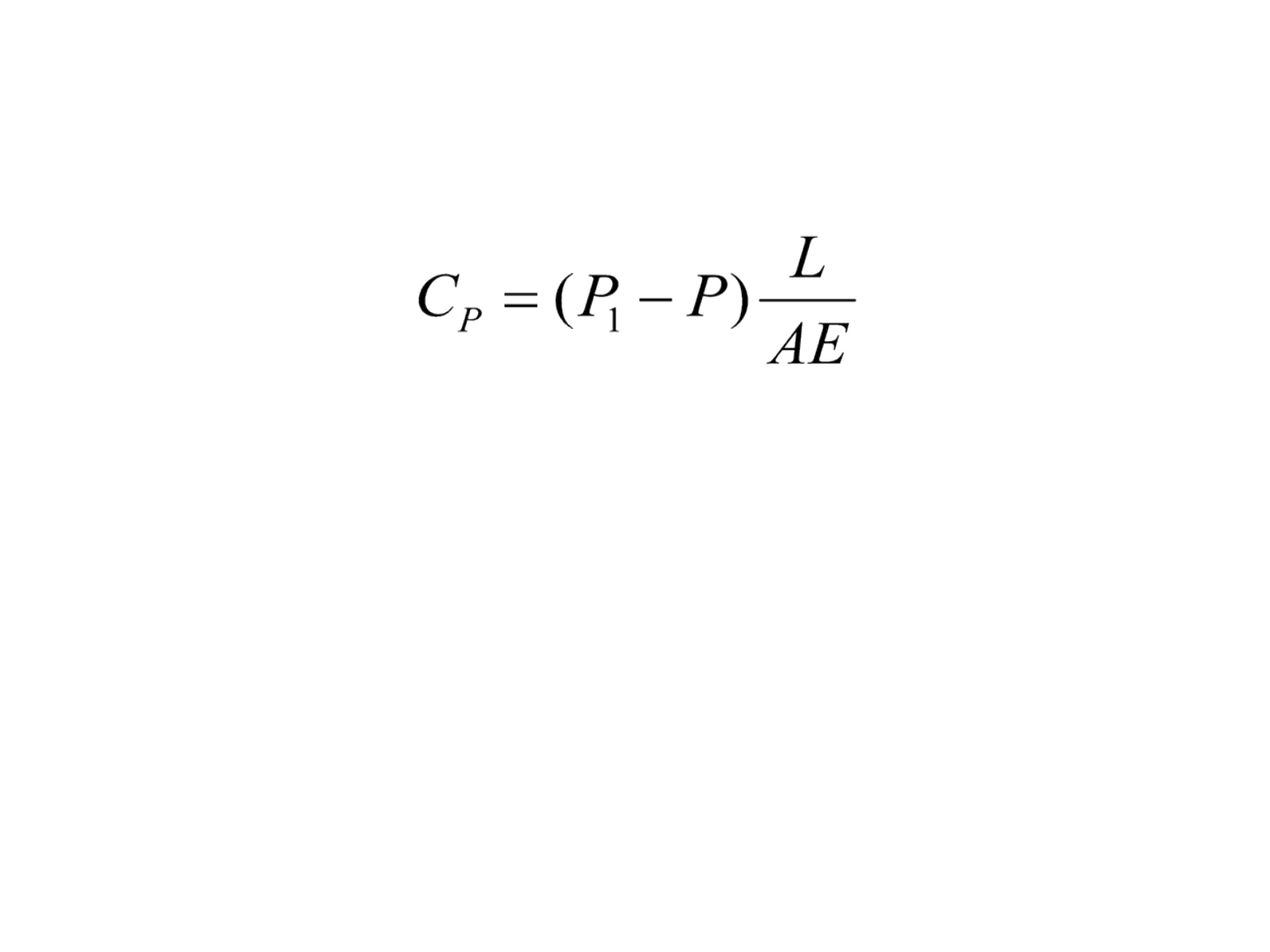
Correções de tensão
• A correção de tensão, C
P
, pode ser calculada por:
• em que C
P
é uma correção positiva (m), P
1
é a
tensão aplicada (kg), P é a tensão padrão (kg), A é a
área da seção transversal (cm
2
), L é o comprimento
da linha observada (m) e E é o módulo de
elasticidade do aço (kg cm
-2
).
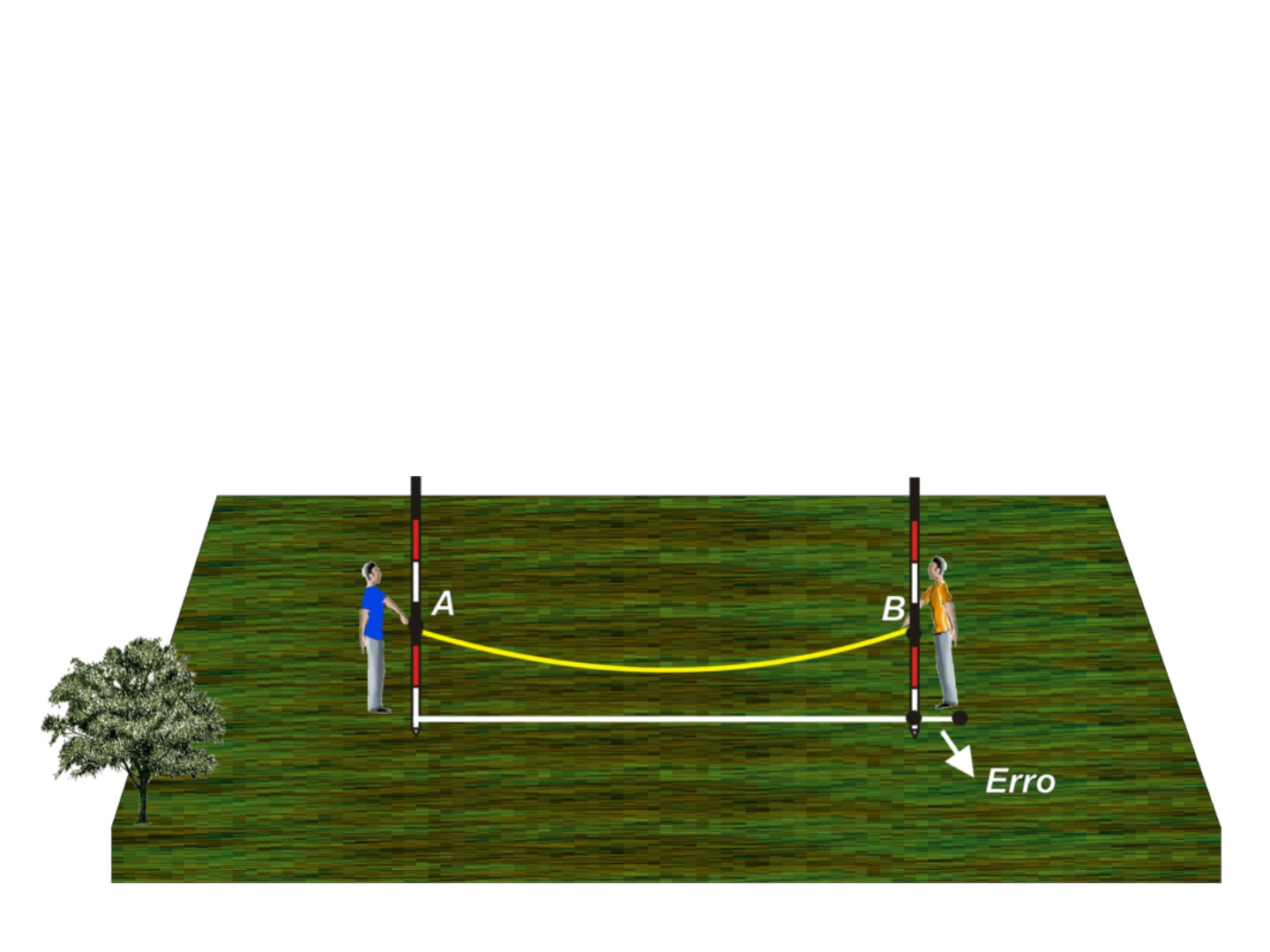
Correções de catenária
• Quando uma trena de aço é segura somente pelas
extremidades, será formada uma curvatura da
trena conhecida por catenária.
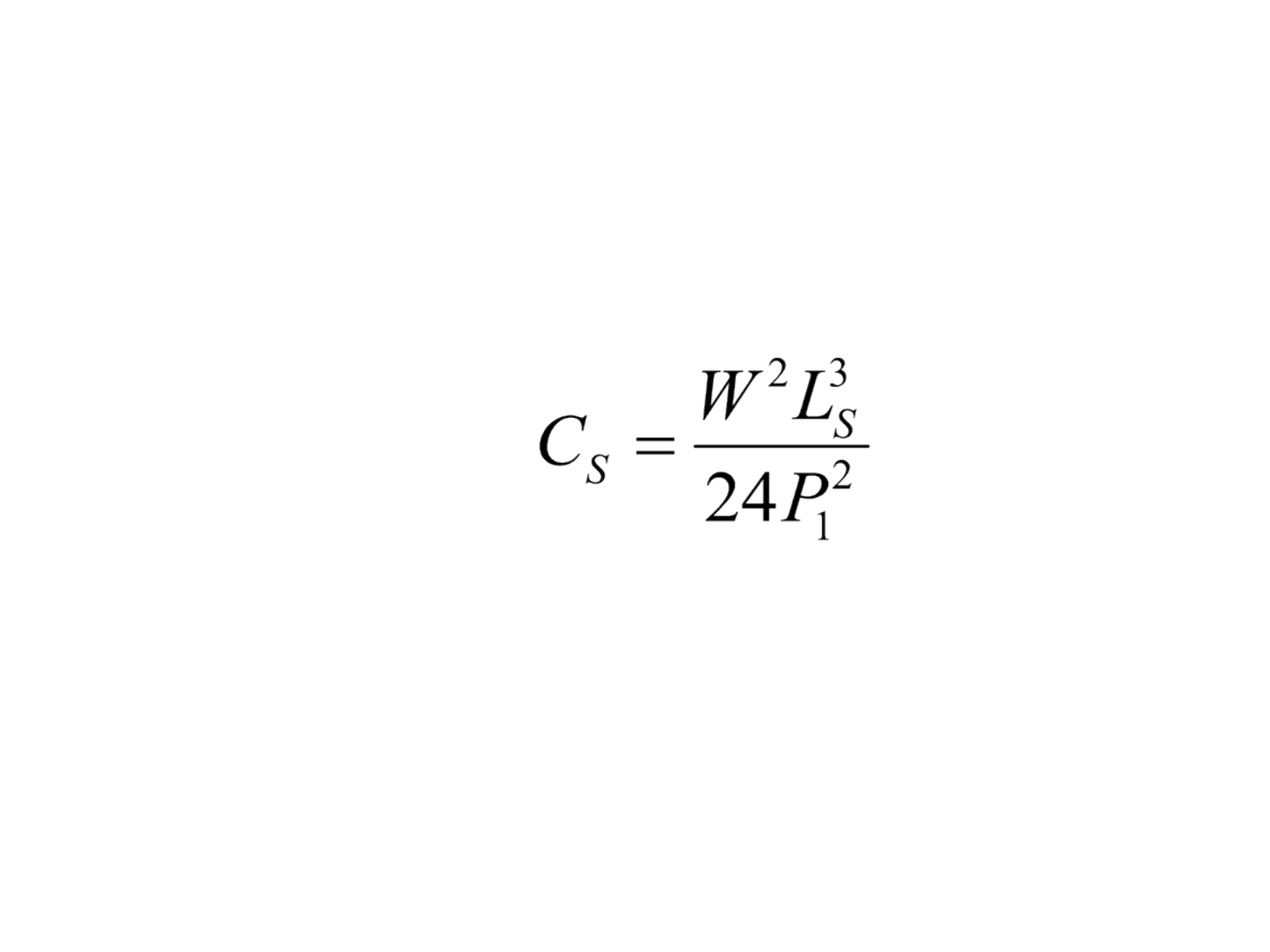
Correções de catenária
• Para corrigir o efeito de catenária, pode-se utilizar
a seguinte correção:
• em que, C
S
é o valor negativo da correção de
catenária (m), L
S
é o comprimento observado (m)
e W é o peso da trena (Kg m
-1
).

Resumo dos erros causados por
levantamento com trena
Tipo de Erro Fonte de Erro
(Instrumental,
Natural,
Humano)
Sistemático
(S) ou
aleatório (A)
Magnitude do erro
Comprimento da trena I S 0,01 m
Temperatura N S ou A 20 ºC
Tensão H S ou A 20 kg
Catenária N, H S 20 cm no centro da linha
Alinhamento H S 1,1 m em uma extremidade
Trena não nivelada H S 1,1 m diferença de altura
Prumo H A 0,01 m
Marcação H A 0,01 m
Leitura H A 0,01 m