
Erros de medição em topografia
Prof. Dr. Marcelo de Carvalho Alves
Departamento de Engenharia
Universidade Federal de Lavras
Lavras, MG

Introdução
• Medição é o interesse principal de um topógrafo;
• Na topografia, o valor exato ou verdadeiro de
uma medição não pode ser determinado;
• Observações básicas: ângulos horizontais e
verticais, distâncias horizontais, inclinadas e
declividade.

• Figura 2.1 Exemplos de medições utilizadas em
topografia.
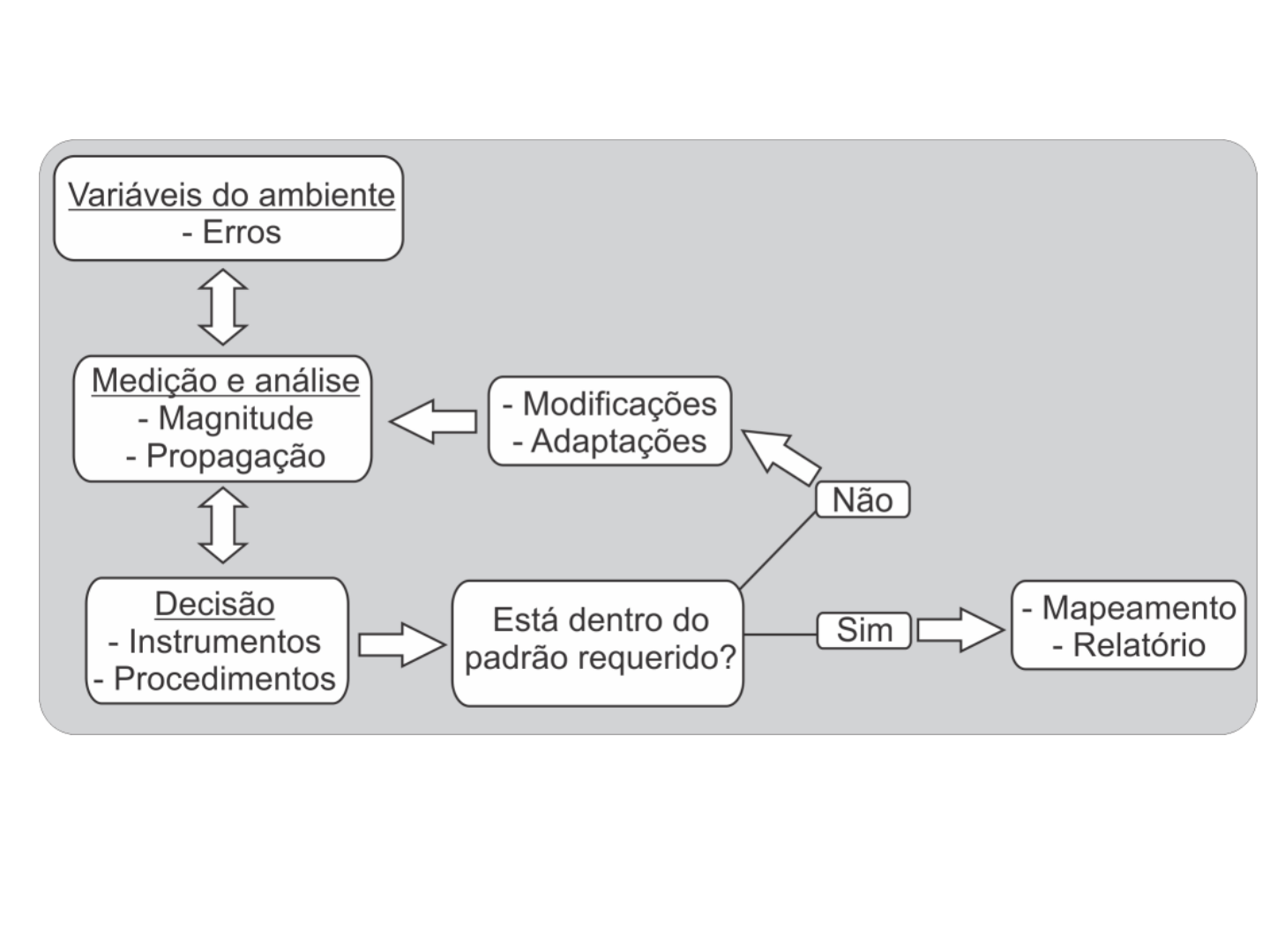
Processo de avaliação de erros
Figura 2.2 Processo decisório em função da avaliação dos
erros de medição.
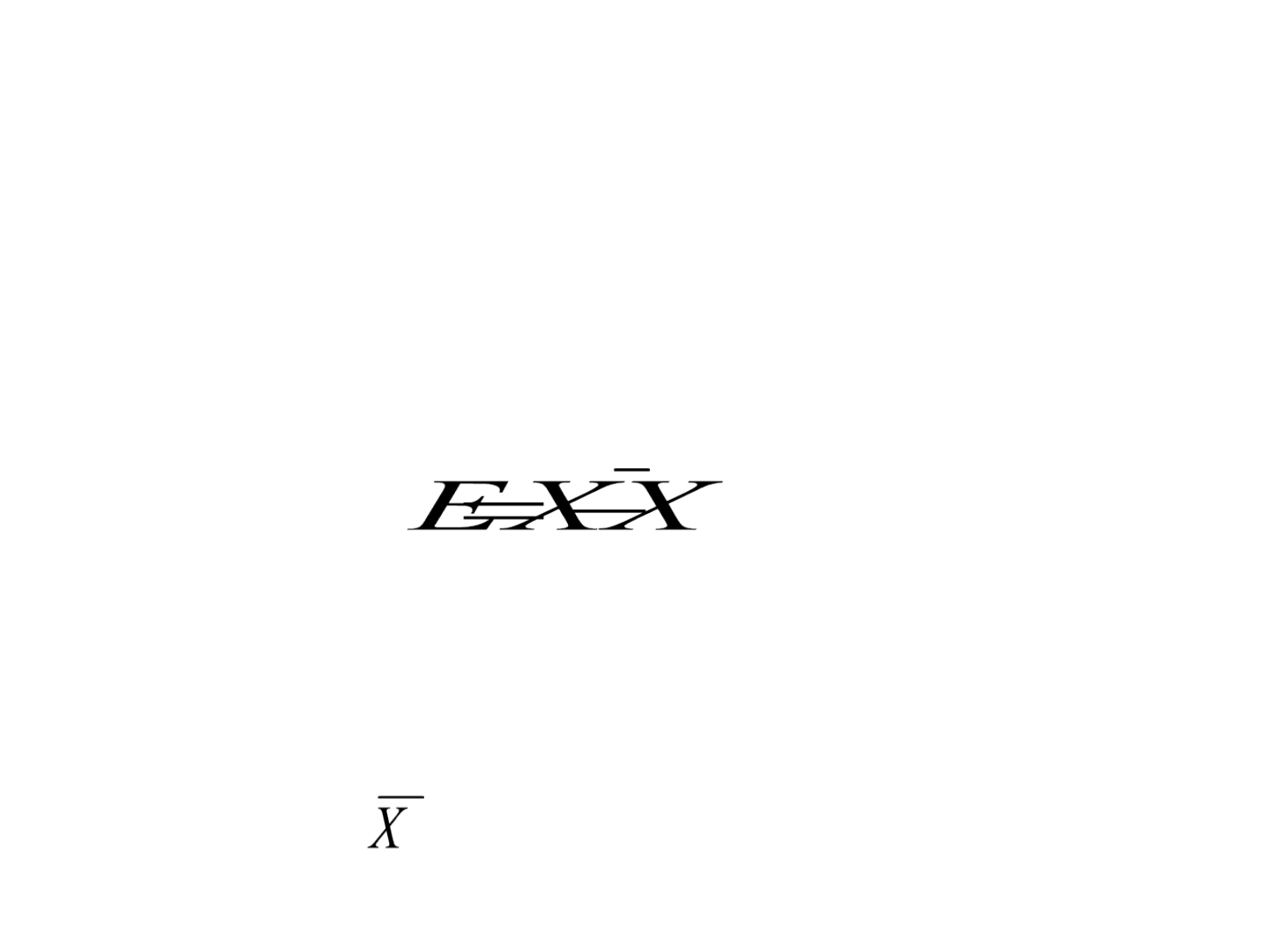
Erros em medições
• O erro é a diferença entre um valor observado de
uma medida quantitativa e o seu valor
verdadeiro:
• em que, E é o erro de uma observação, X , o valor
observado e , o valor verdadeiro.

Erros em medições
• Pode-se afirmar que:
• (1) Nenhuma observação é exata,
• (2) Toda observação contém erros,
• (3) O erro exato presente é sempre desconhecido.
**Mesmo com o melhor equipamento desenvolvido,
observações mais próximas de seu valor verdadeiro
nunca serão exatas.

Fontes de erros de medições
• Naturais.
• Instrumentais.
• Humanos.

Tipos de erros de medições
• Enganos.
• Erros sistemáticos.
• Erros aleatórios.

Acurácia, precisão e resolução
• Discrepância é a diferença entre dois valores
observados da mesma medição.
• Precisão é o grau de refinamento de observações
com base no tamanho da discrepância.
• Acurácia é a proximidade de uma medição ao
valor verdadeiro.
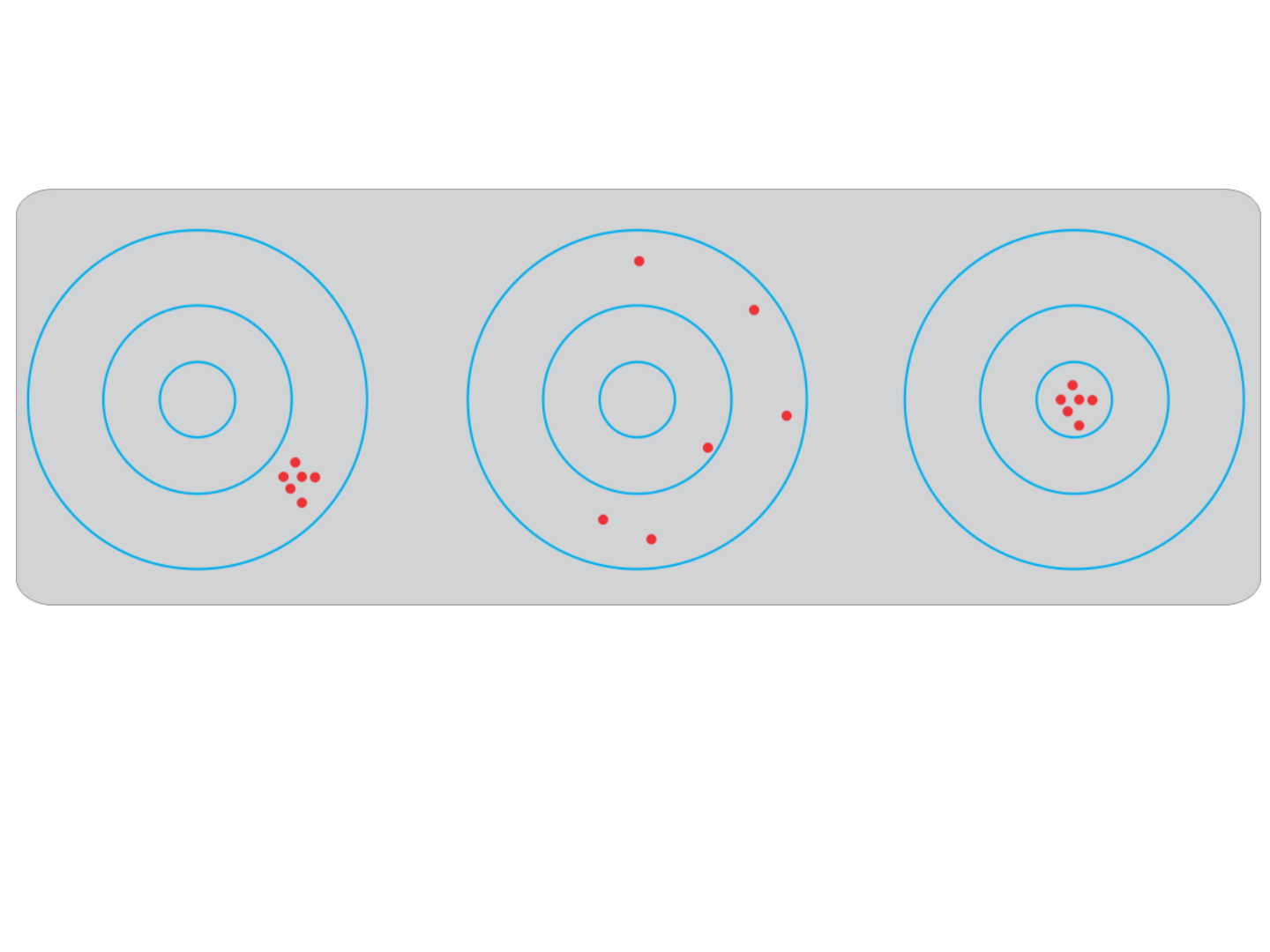
Acurácia, precisão e resolução
Figura 2.3 Acurácia e precisão de um arqueiro quando o objetivo é
acertar o centro do alvo. Boa precisão e ruim acurácia (esquerda), ruim
precisão e acurácia (centro), boa precisão e boa acurácia (direita).
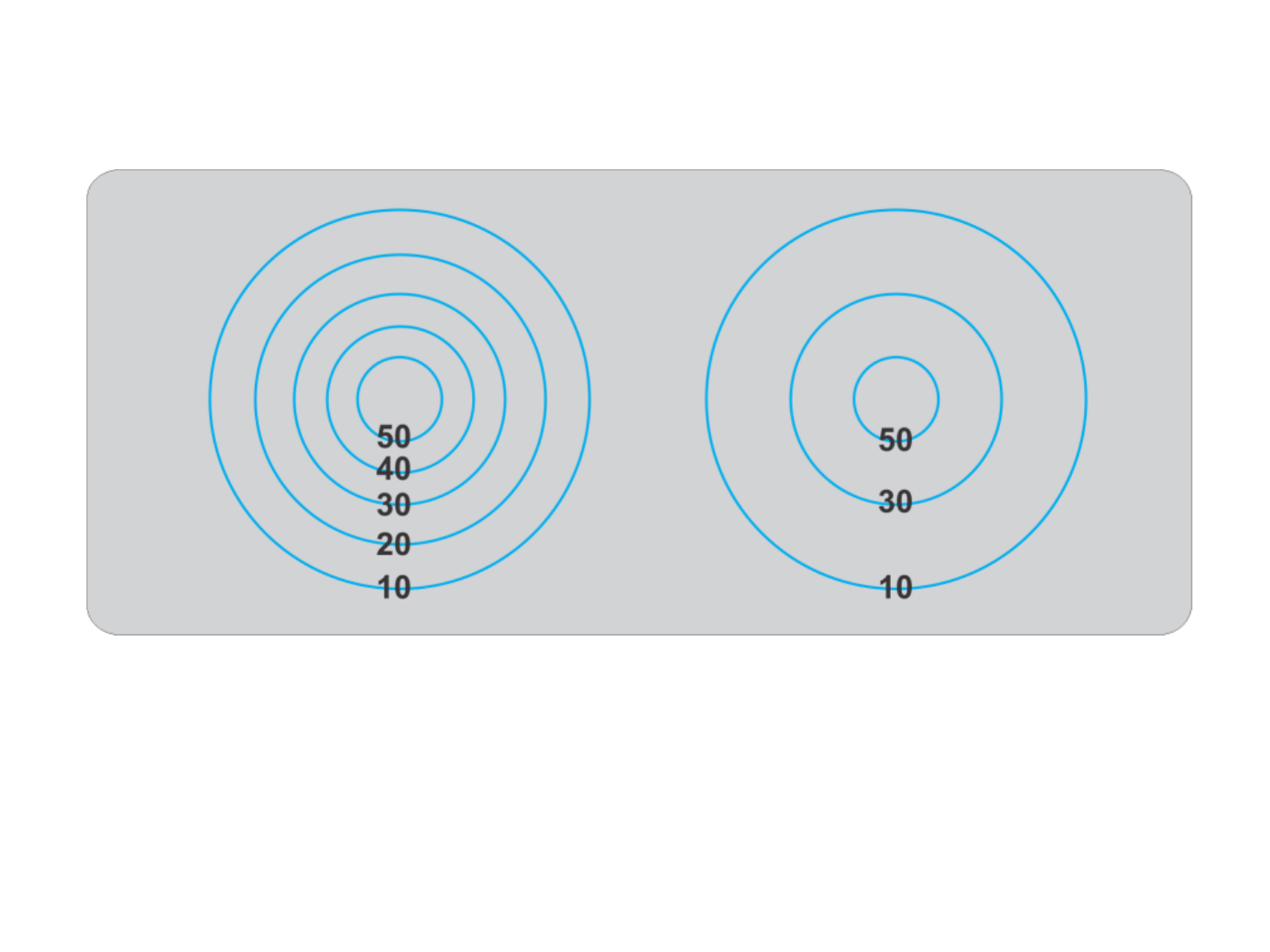
Acurácia, precisão e resolução
Figura 2.4 Resolução de alvos utilizados pelo arqueiro. O alvo da
esquerda apresentou maior número de subdivisões e maior
resolução.

Eliminação de enganos
• Realizar repetições da mesma medição.
• Observar o valor discrepante e eliminar.
• A manipulação dos dados é uma prática ilícita e
pode causar problemas.

Eliminação de erros sistemáticos
• Os erros sistemáticos podem ser calculados e
corrigidos.
• Realizar visadas de vante e ré entre os mesmos
pontos.
• Medir ângulos em diferentes posições da luneta.

Probabilidade
• Taxa referente ao número de vezes que um resultado
pode ocorrer em relação ao número total de
possibilidades.
• Se um resultado m não ocorrer n vezes, a probabilidade
de ocorrência deste resultado é m / (m + n).
• A probabilidade de um resultado deve variar entre 0 e
1, sendo 0 a impossibilidade e 1, a absoluta certeza.

Probabilidade
• A soma das probabilidades de ocorrência ou falha de
um resultado deve ser 1.
• Se 1/4 é a probabilidade de acerto de uma resposta na
prova, então, a probabilidade de erro da resposta é [(4-
1)/4] ou 3/4.
• A teoria de probabilidade é aplicada ao estudo dos
erros aleatórios, após remover enganos e erros
sistemáticos.
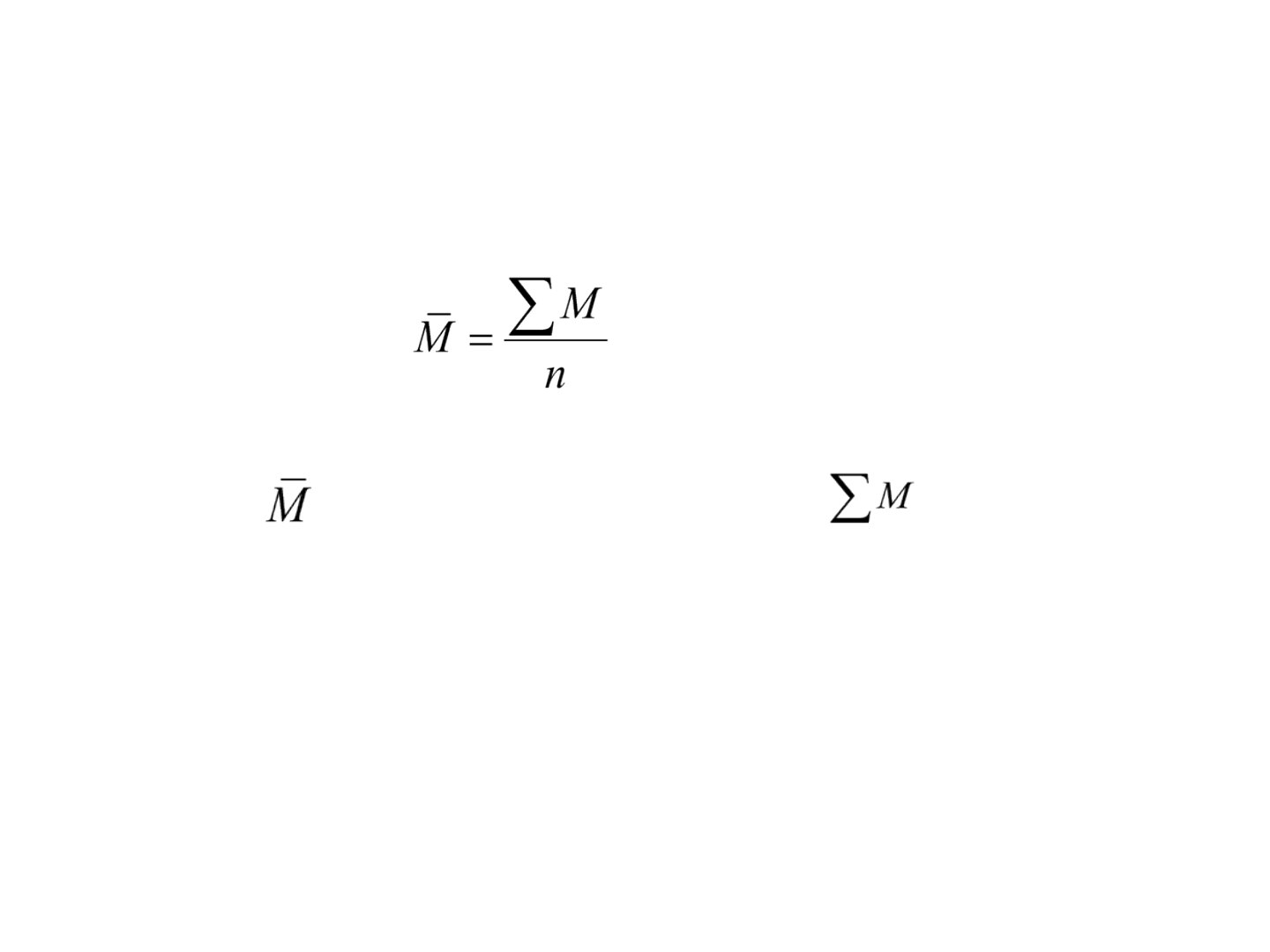
Valor mais provável
• O valor mais provável é:
• em que, é o valor mais provável, é a soma das
medições individuais M e n, o total de observações
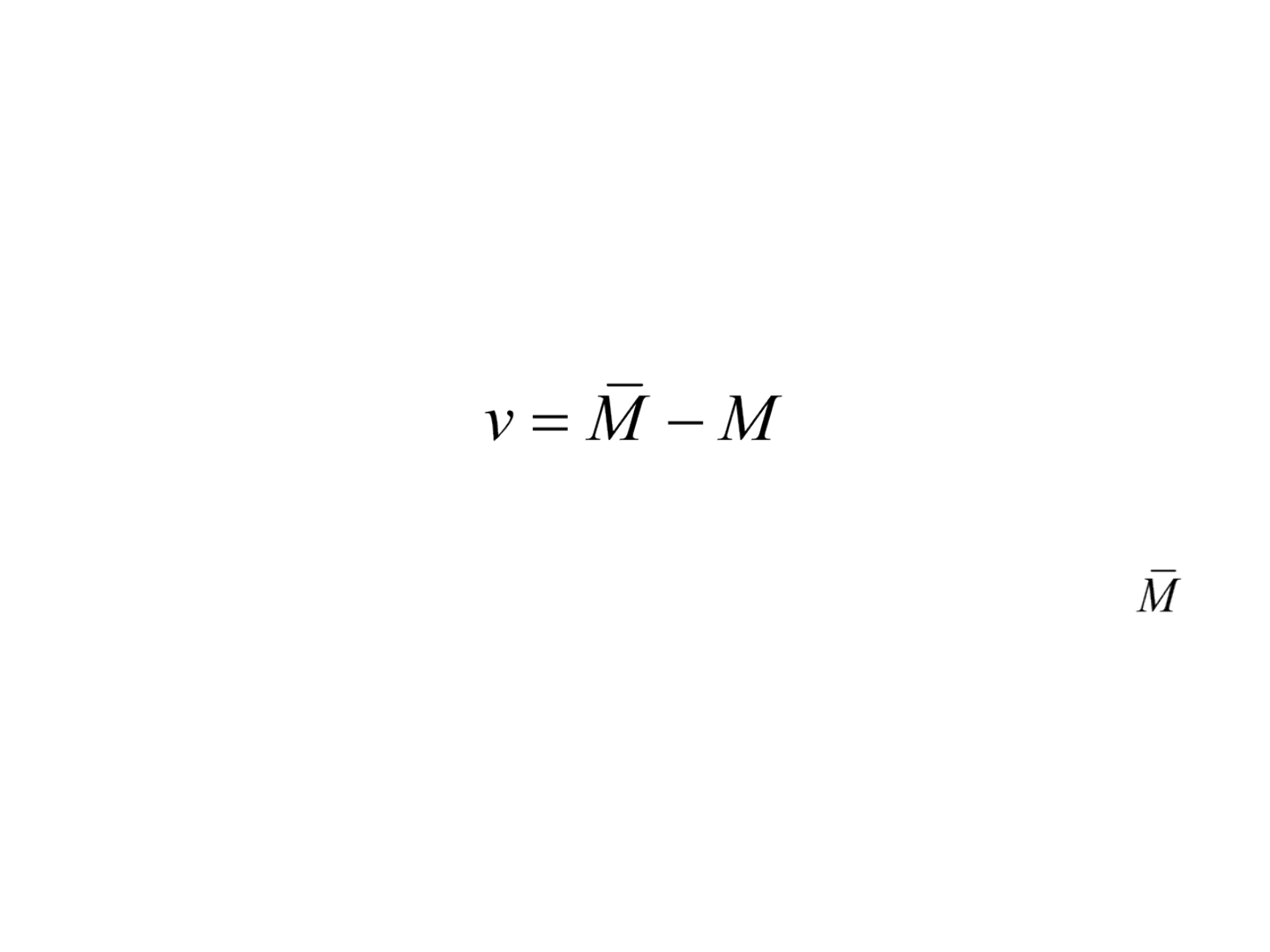
Resíduos
• O resíduo é a diferença entre o valor mais provável e
outro valor medido:
• em que, v é o resíduo de qualquer observação M, e é
o valor mais provável da medição.

Ocorrência de erros aleatórios
• O histograma é um gráfico de barras que representa o
tamanho das observações em relação à frequencia de
ocorrência.
• Com isso é possível obter uma impressão visual do
padrão de distribuição das observações ou dos resíduos.
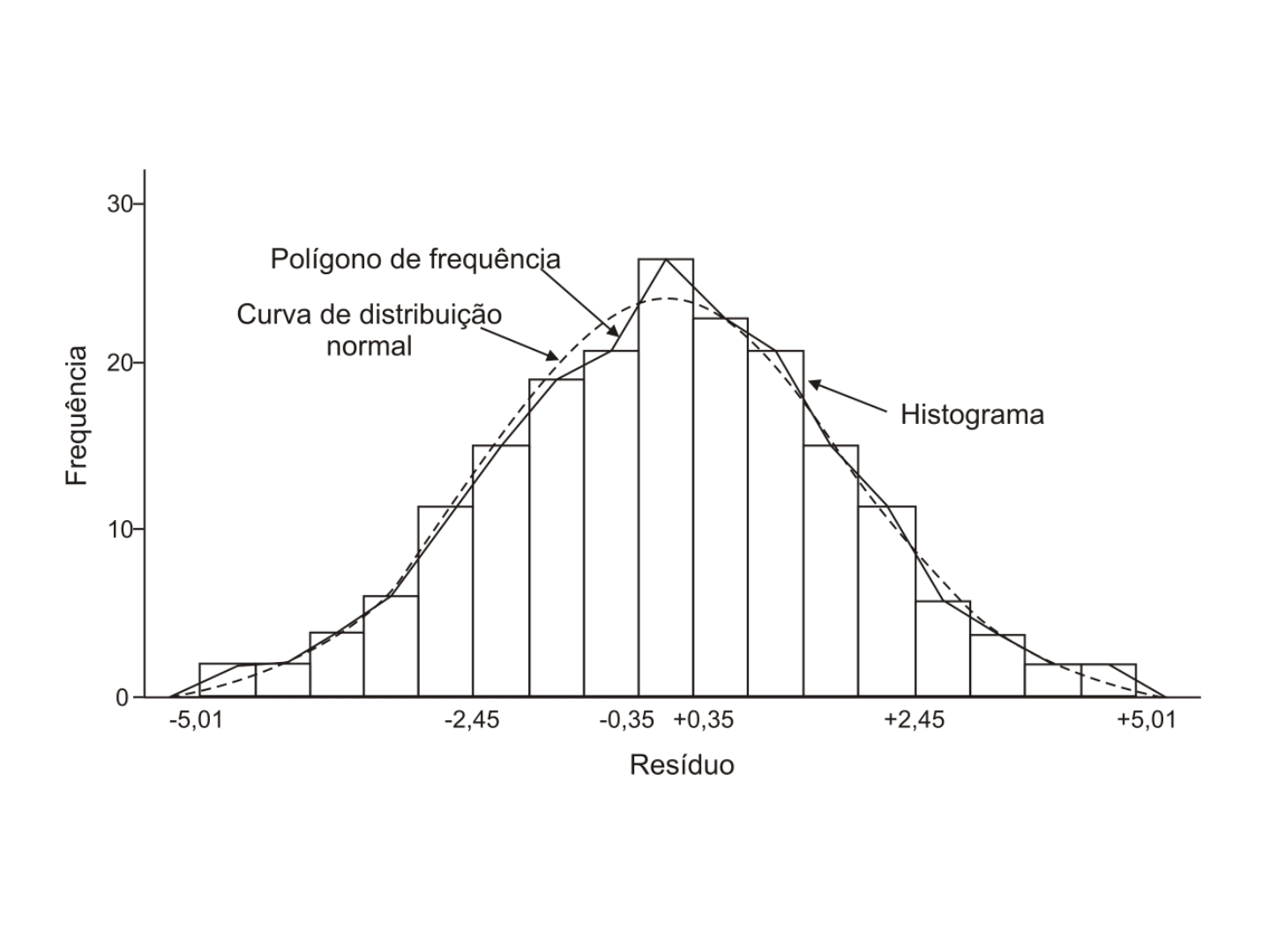
Ocorrência de erros aleatórios
Figura 2.5. Histograma de frequência com curva de distribuição normal
dos resíduos a partir de distâncias horizontais medidas com estação
total eletrônica.
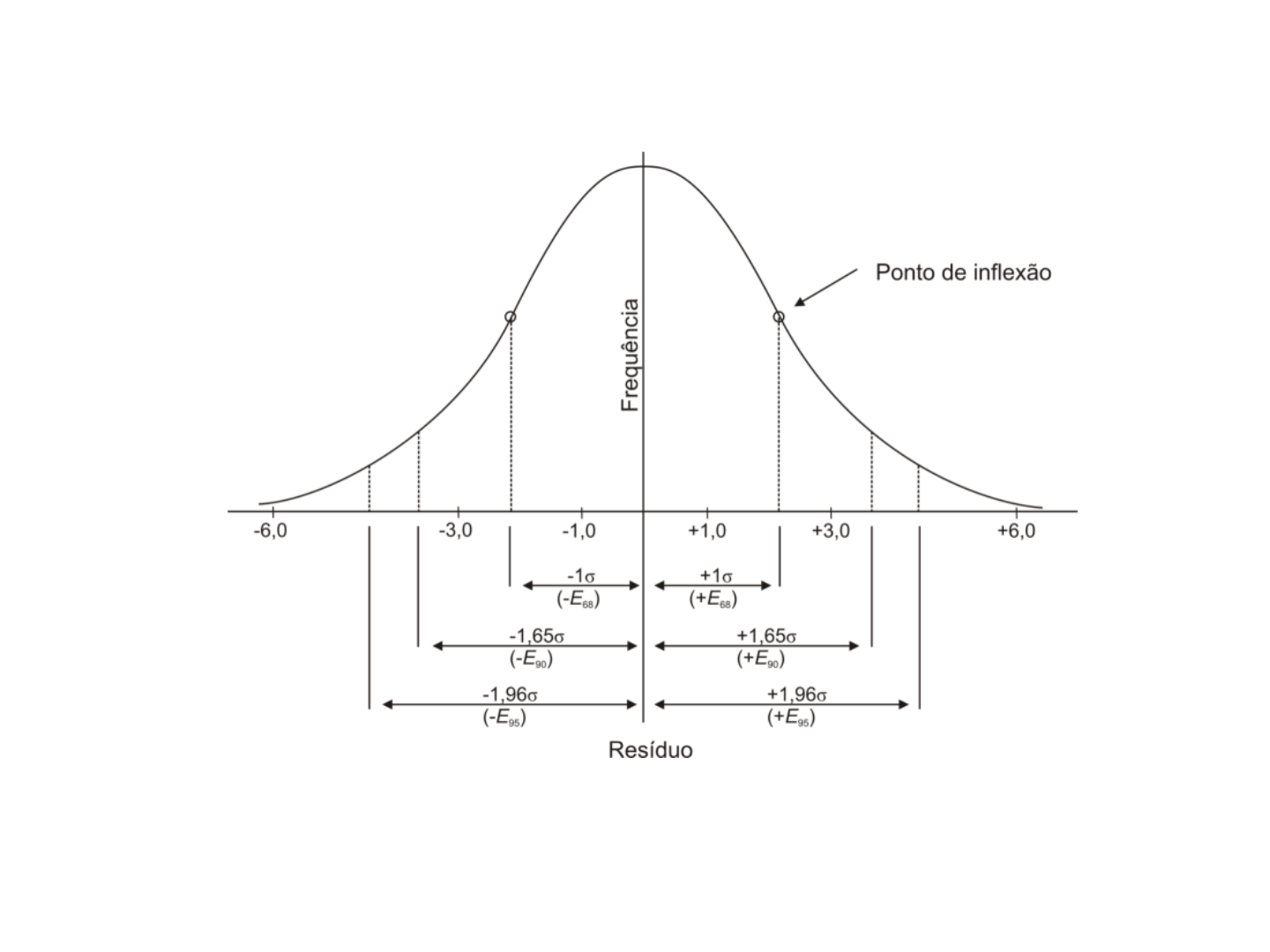
Ocorrência de erros aleatórios
Figura 2.6. Curvas de distribuição normal utilizadas para comparar a
precisão de levantamentos.
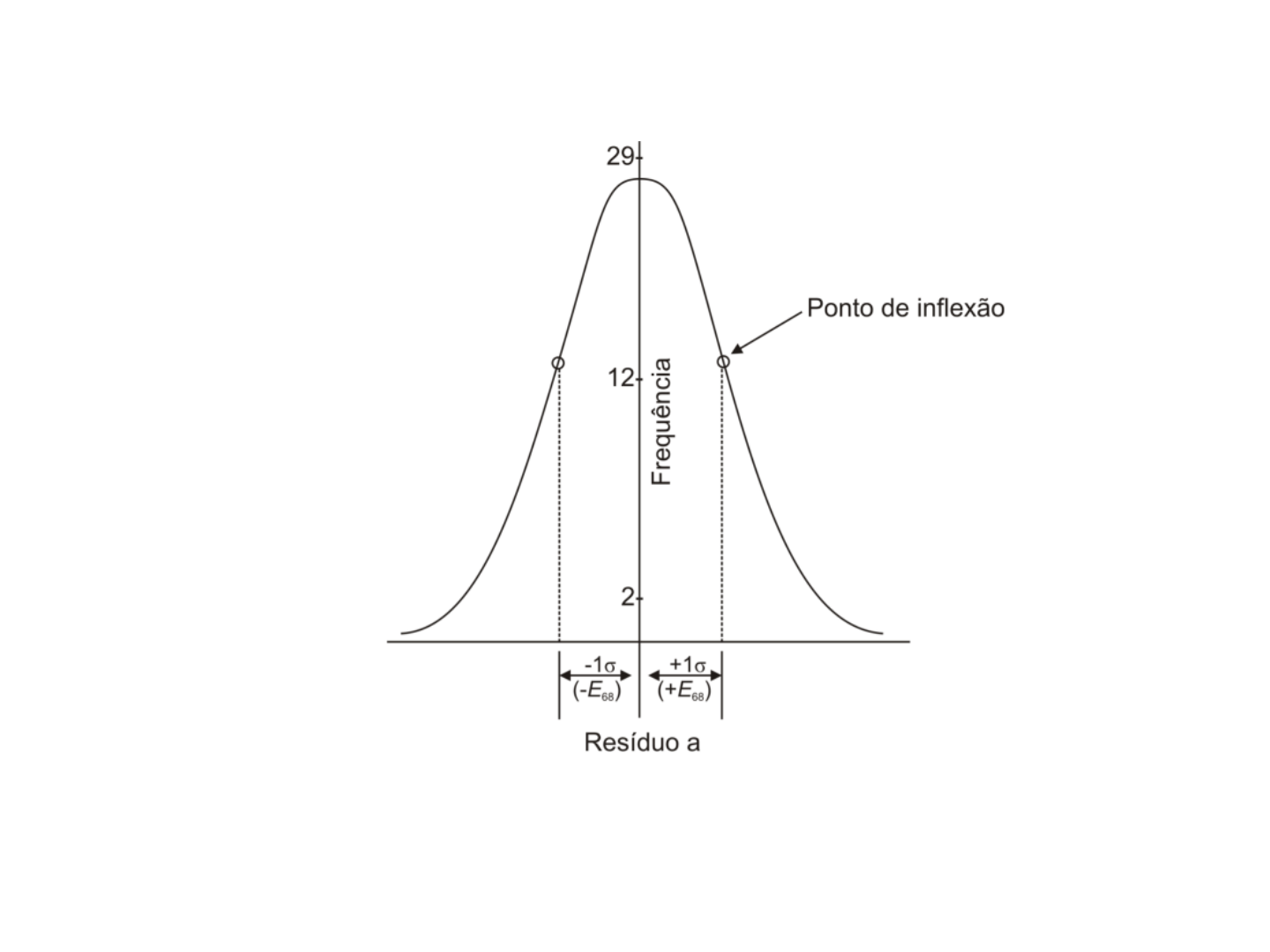
Ocorrência de erros aleatórios
Figura 2.7a Curva de distribuição normal para dados com maior
(Resíduo a) precisão.
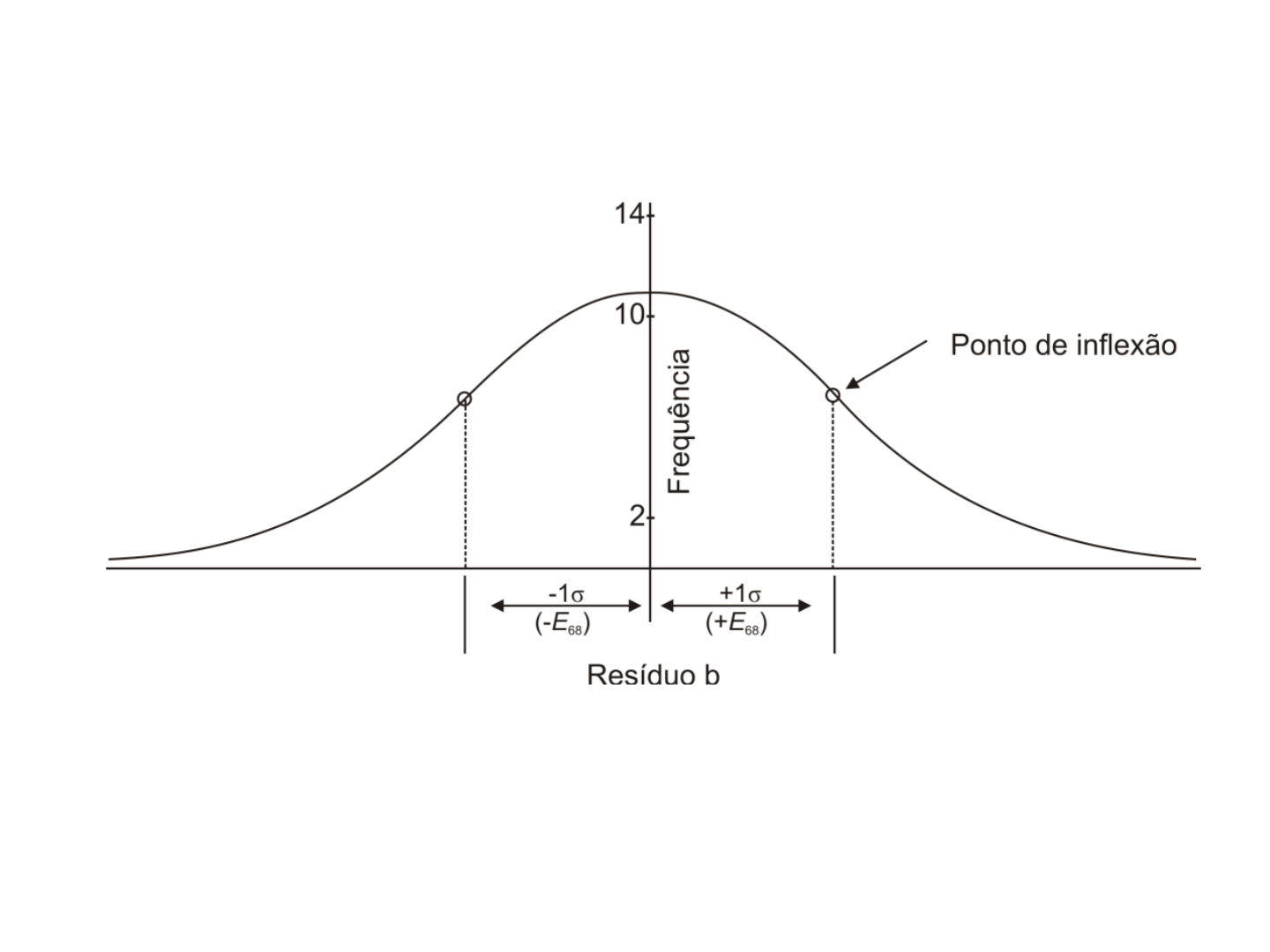
Ocorrência de erros aleatórios
Figura 2.7b Curva de distribuição normal para dados com menor
(Resíduo b) precisão.

Leis gerais de probabilidade
• Resíduos pequenos ocorrem com maior freqüência do que
os grandes, ou seja, resíduos pequenos são mais prováveis.
• Grandes erros são menos freqüentes e, portanto, menos
prováveis. Portanto, valores maiores são mais enganos do
que erros aleatórios.
• Erros positivos e negativos do mesmo tamanho ocorrem
com frequência igual e, portanto, com probabilidade igual,
ou seja, o valor mais provável é a média.
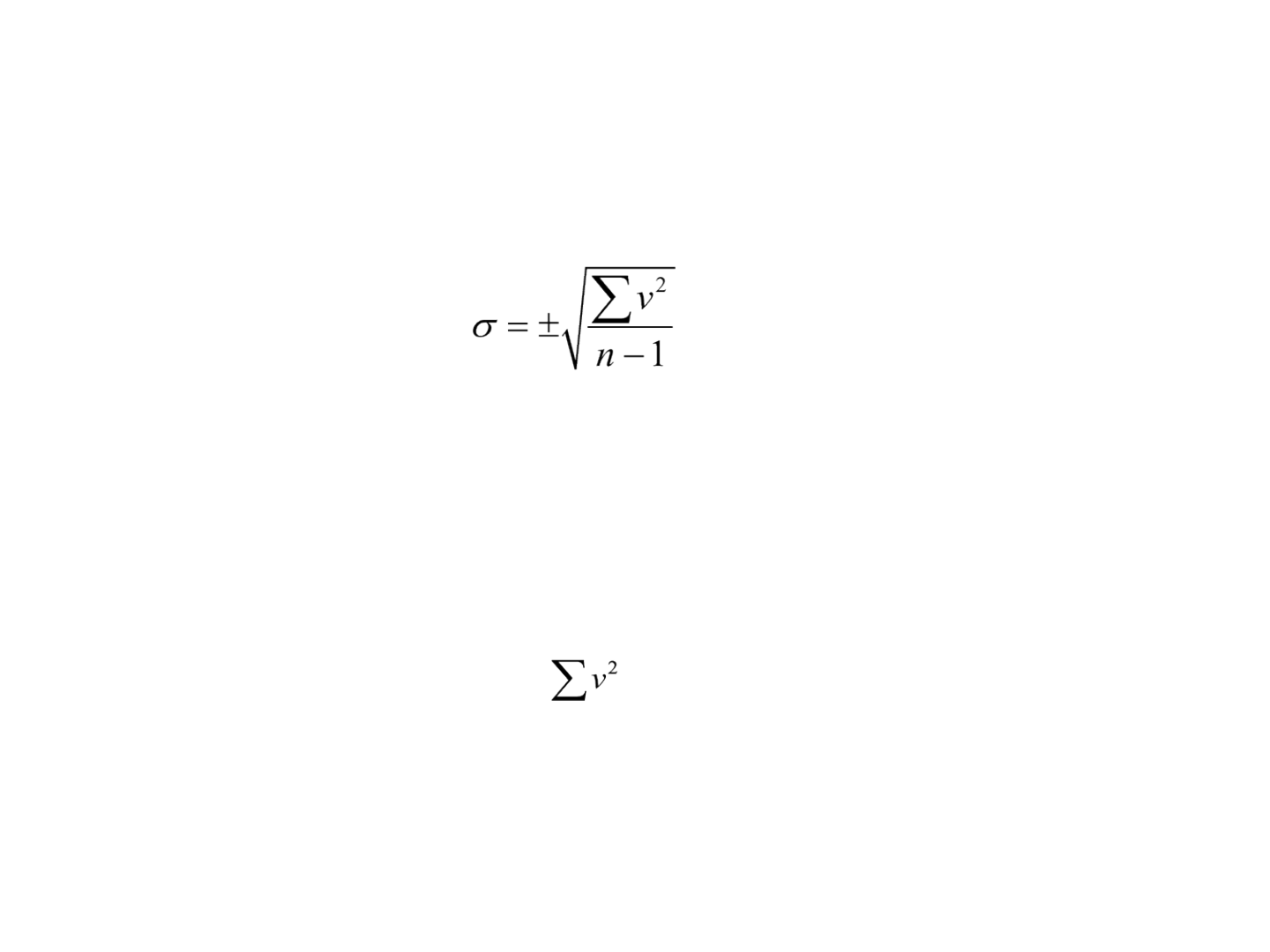
Medidas de precisão
• A equação do desvio padrão pode ser definida por:
• em que, σ é o desvio padrão de um grupo de
observações da mesma medição, v é o resíduo de uma
observação individual, é a soma de quadrados dos
resíduos individuais e n, o número de observações.
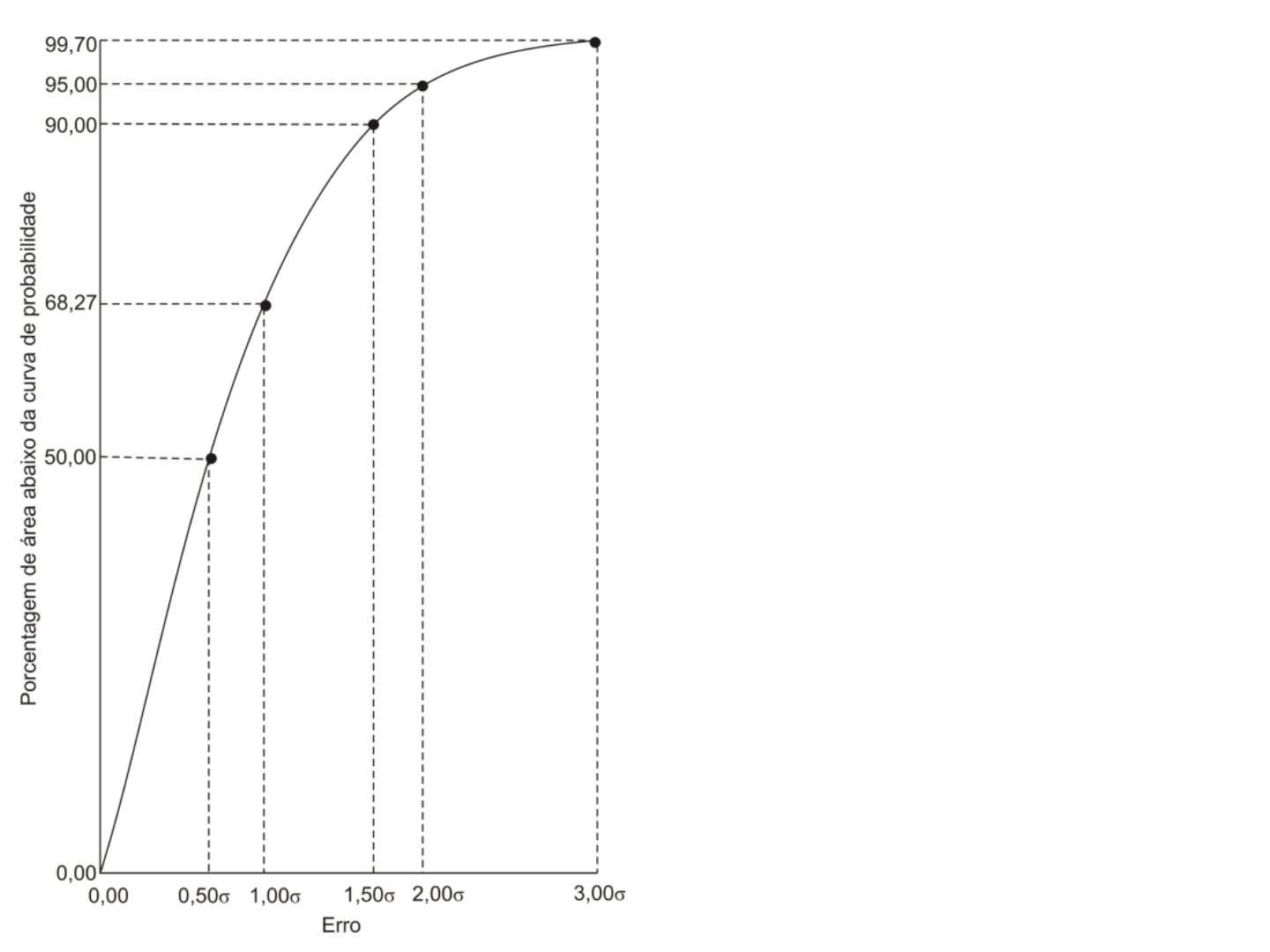
Medidas de precisão
Figura 2.9. Relação entre erro e
porcentagem da área abaixo da
curva de distribuição normal.

Interpretação do desvio padrão
• Se uma observação fosse repetida 10 vezes, para uma
porcentagem de probabilidade de 68,3%, seria
esperado que aproximadamente 7 resultados
ocorressem dentro dos limites estabelecidos pelo
desvio padrão e 3 resultados fora desses limites.
• Uma observação adicional terá 68,3% de probabilidade
de cair dentro do limite configurado pelo desvio padrão.
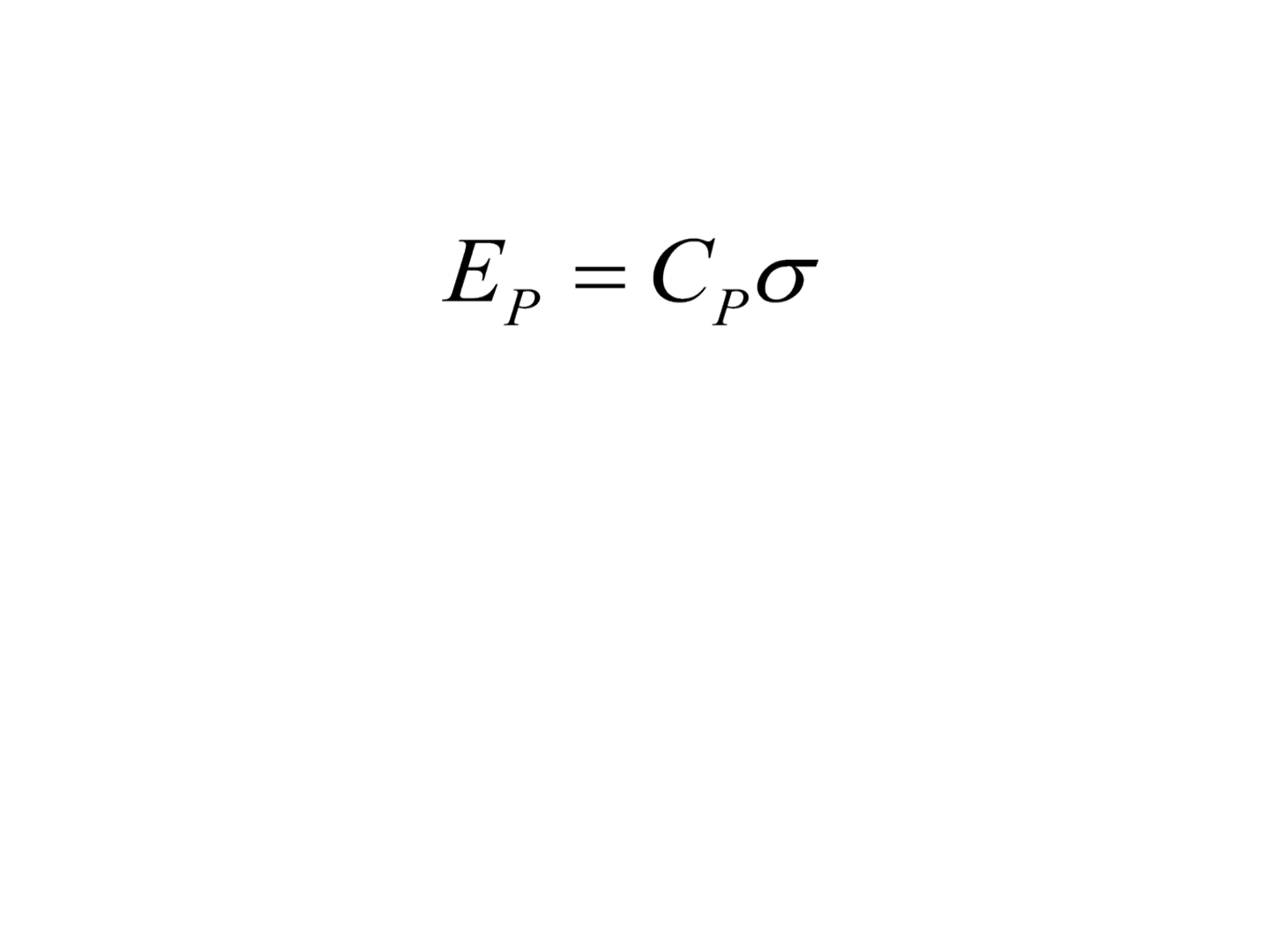
Erros de 50%, 90% e 95%
• em que, E
P
é uma determinada porcentagem de
erro e C
P
, o fator numérico correspondente
obtido pela relação o erro e a porcentagem da
área abaixo da curva de distribuição normal.
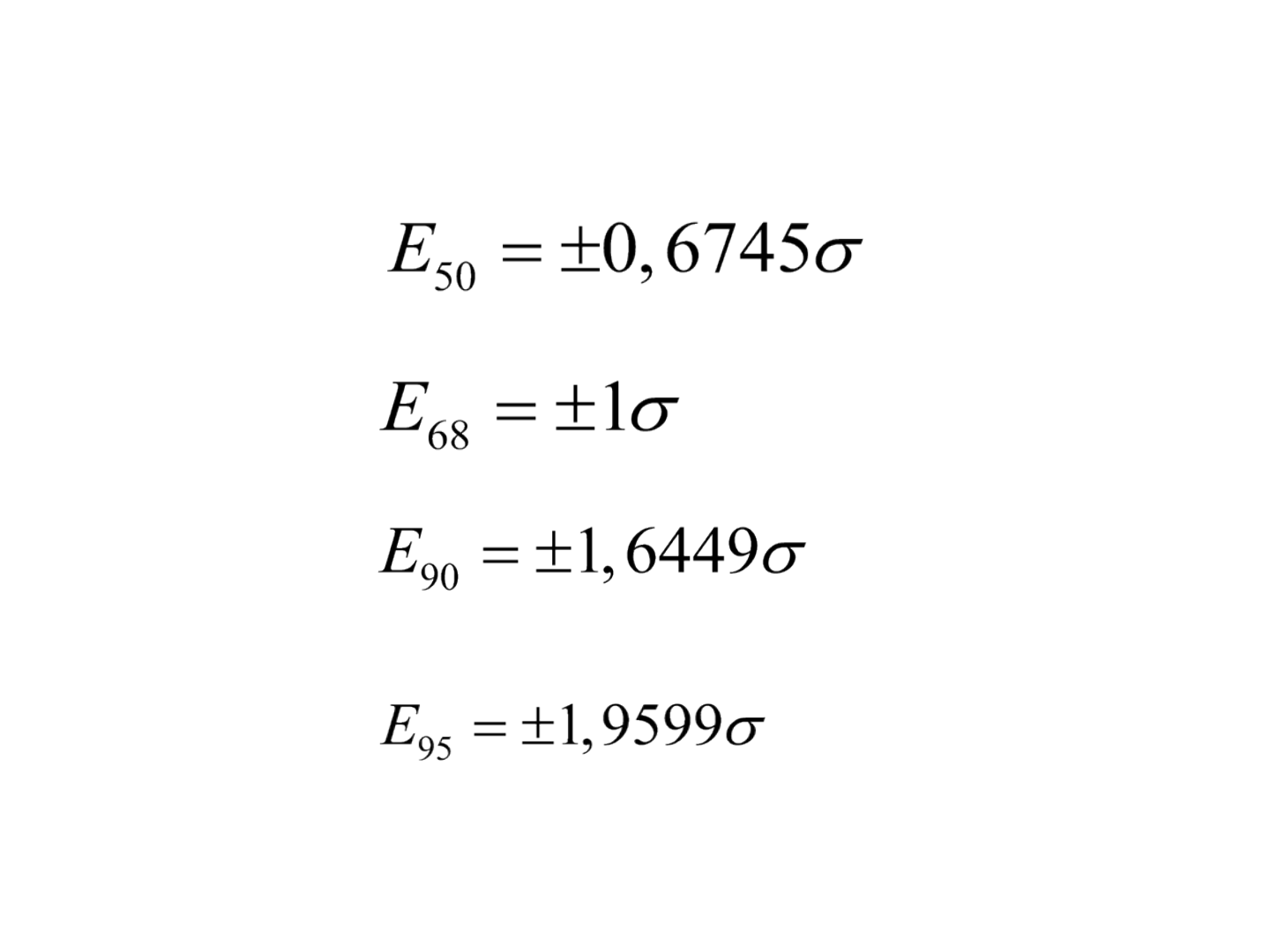
Erros de 50%, 90% e 95%

Erros de 50%, 90% e 95%
• O erro de 50% é denominado de erro provável.
• Os erros de 90% e 95% são normalmente utilizados para
especificar precisão requerida em projetos de
levantamento. Erro de 95%, também denominado de
erro 2 sigma (2σ), é o mais utilizado.
• Se o resíduo for maior que 3 σ , pode-se considerar a
medição como um engano.
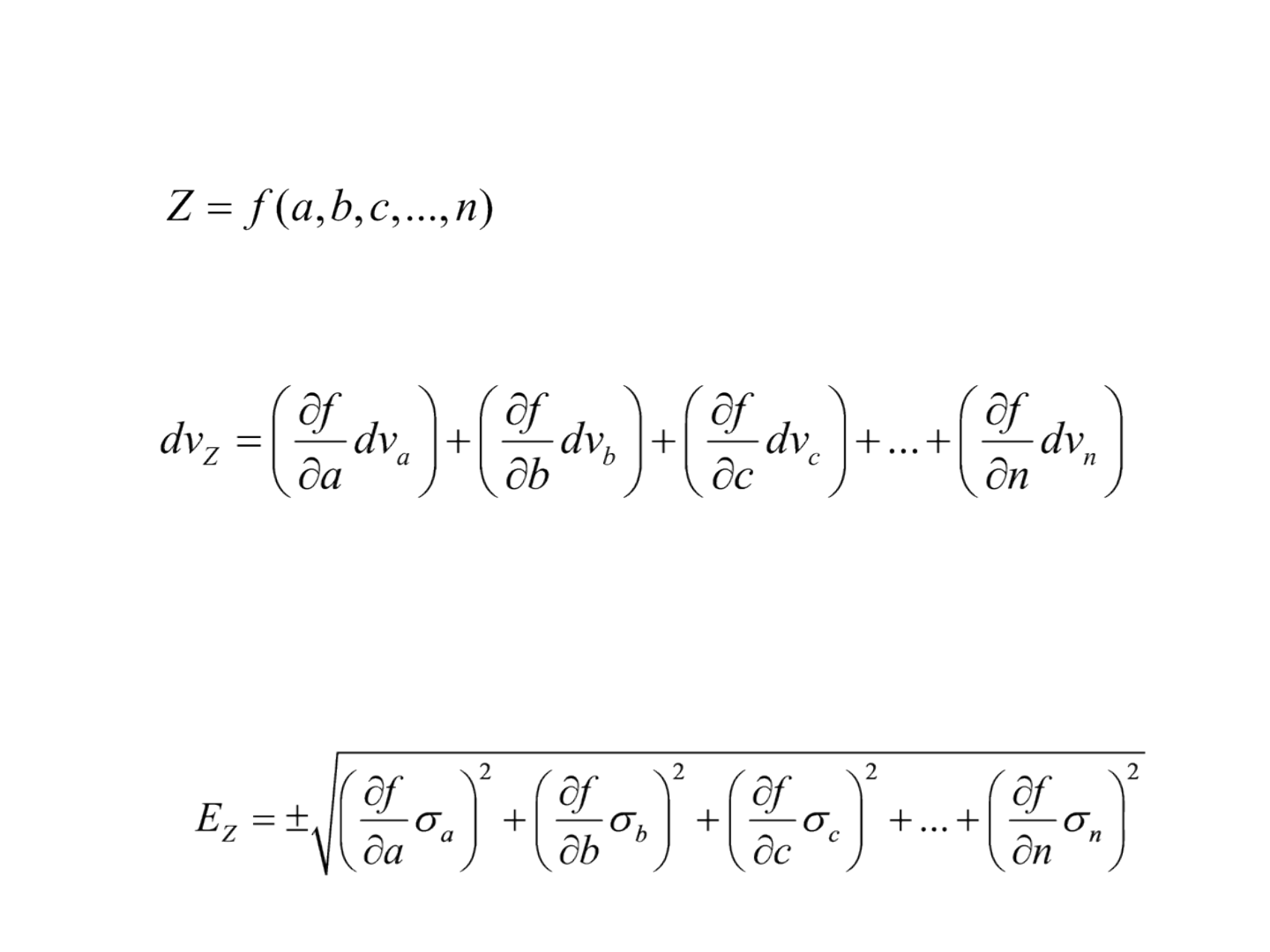
Propagação do erro
• Se , em que Z é uma medida derivada
das observações a, b, c,...,n, o erro em Z é:
• Se a, b, c,...,n, são observações independentes, o desvio
padrão em Z é:
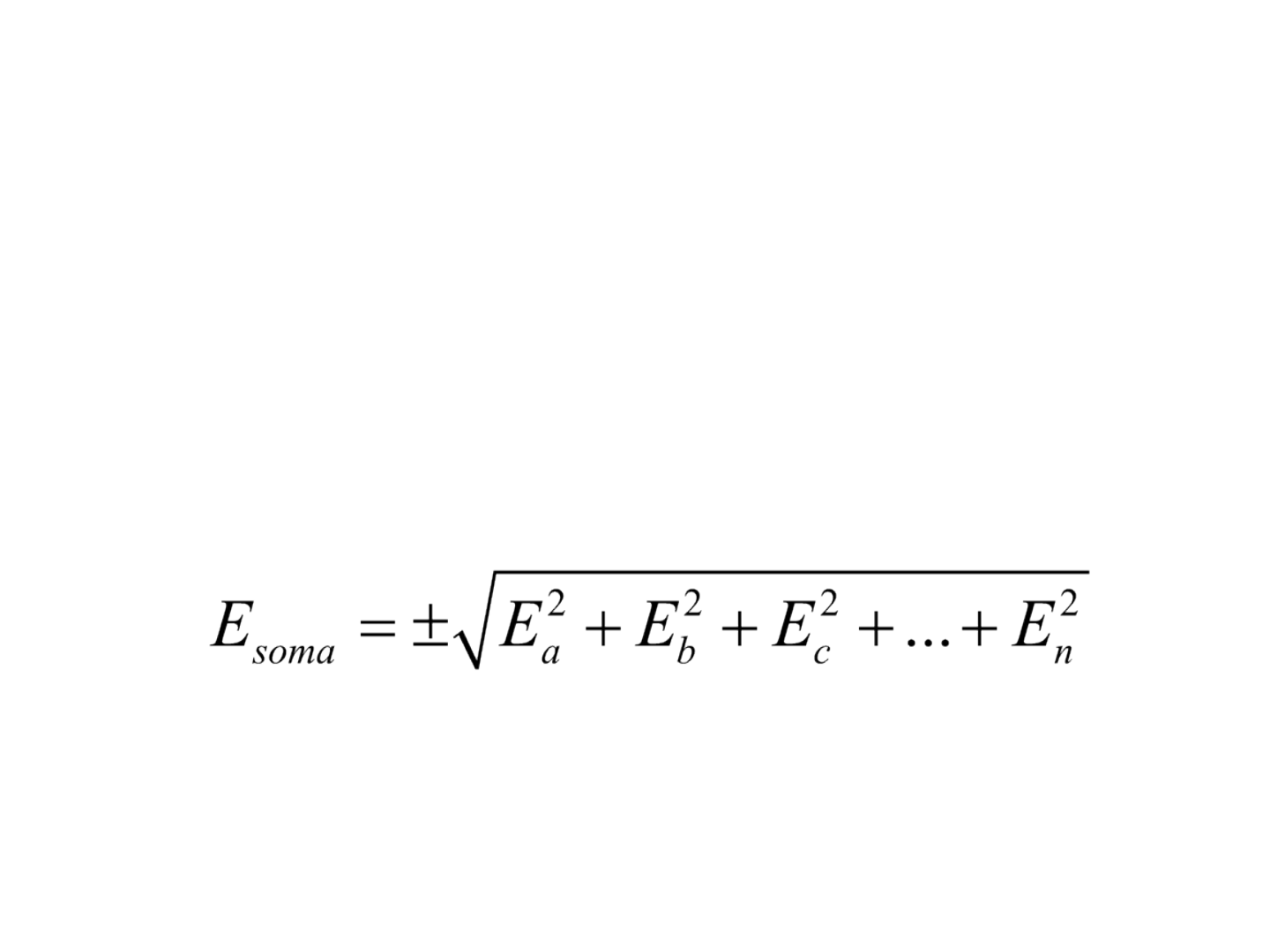
Erro de uma soma
• Considerando-se que a soma de observações
independentes a, b, c,...,n, o erro propagado em relação
à soma das medições contendo diferentes erros
aleatórios é:
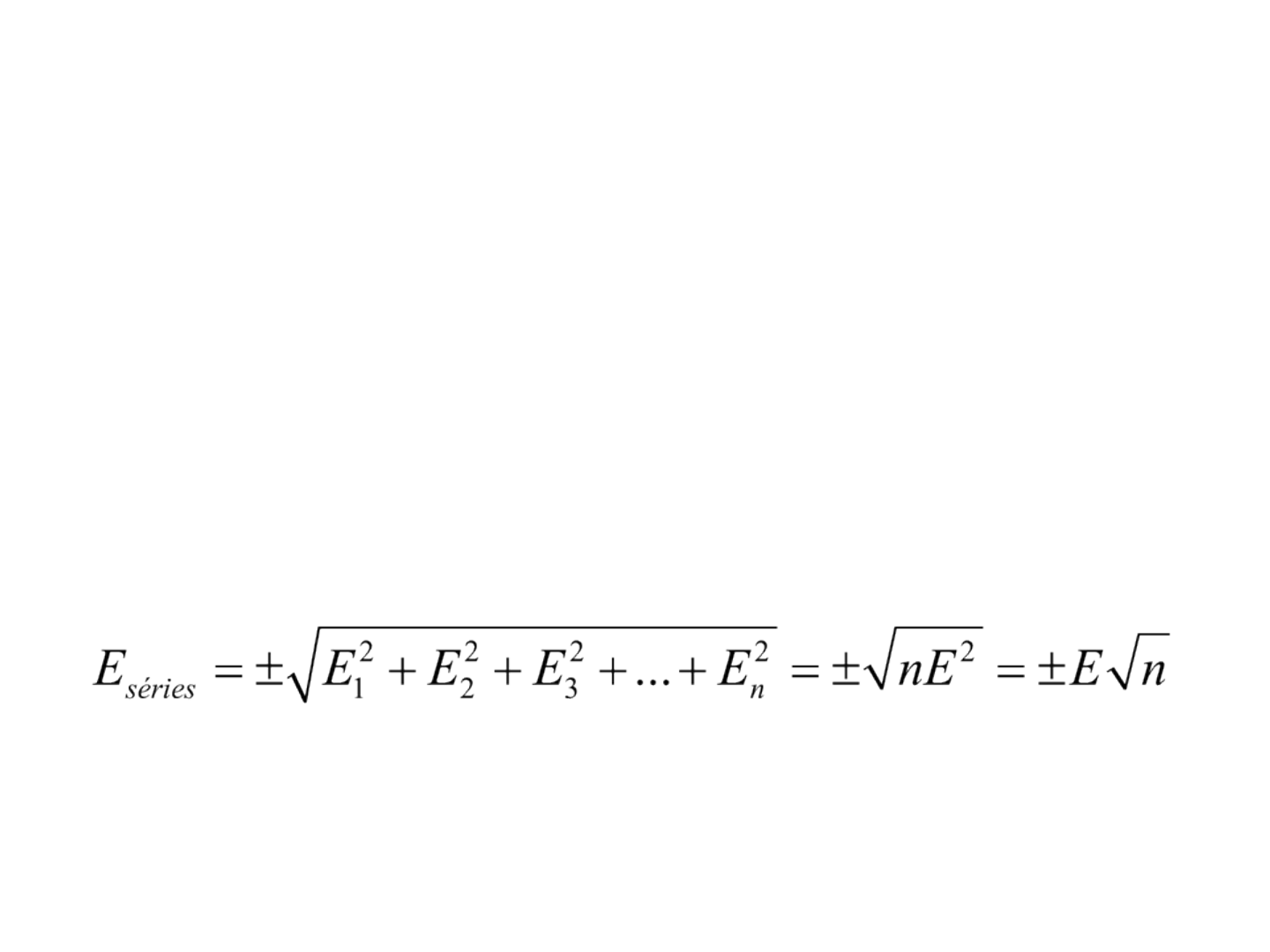
Erro de uma série
• Esse tipo de erro só pode ser considerado se todas as
medições forem feitas com igual precisão e
confiabilidade. O erro total da soma de todas essas
medidas em série é denominado de erro de uma série:
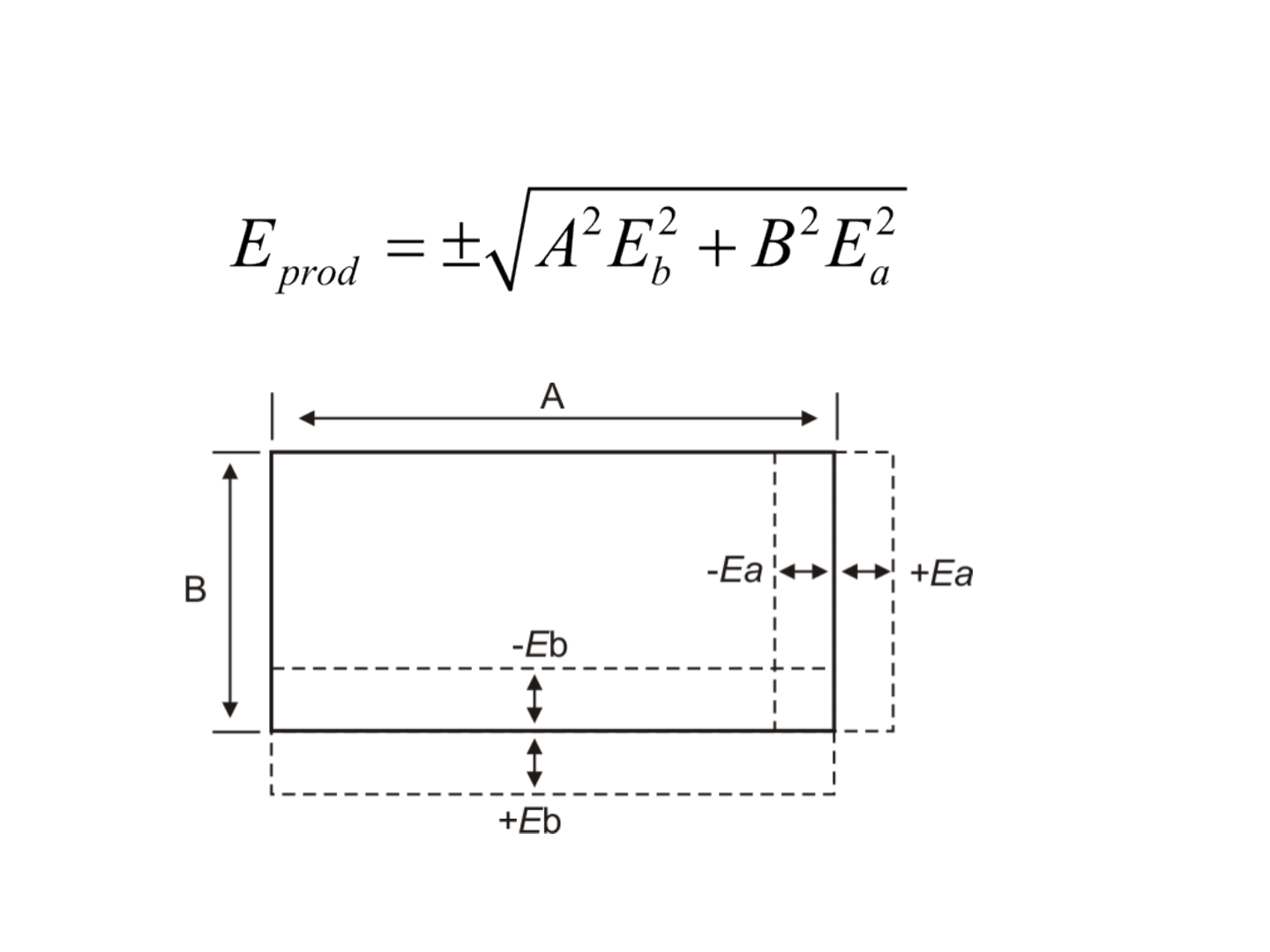
Erro de um produto
Figura 2.10. Erro de uma área.
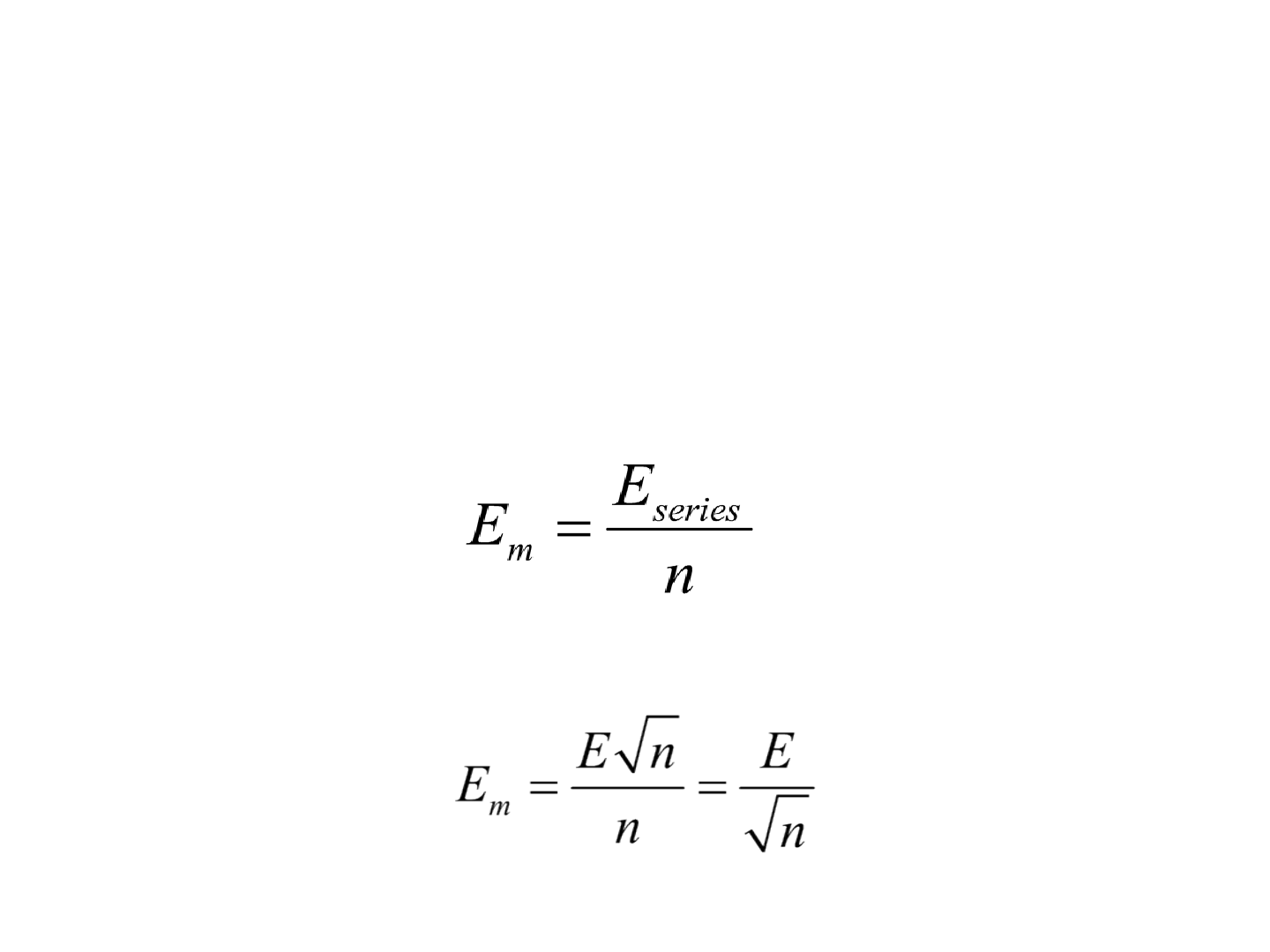
Erro de uma média
• Como a soma dividida pelo número de observações
fornece uma média, o erro da média pode ser
encontrado pela relação:
• Substituindo:

Erro de uma média
• O erro de uma média pode ser aplicado a uma
porcentagem de probabilidade:

Aquisição eletrônica de dados
• Coletoras de dados podem receber e armazenar dados
automaticamente em arquivos compatíveis com
computadores.
• A transferência dos dados pode ser realizada por
cartões de memória ou cabos.
• Pode-se evitar enganos, reduzir tempo de
processamento, visualização e arquivamento de notas
de campo no escritório.

Aquisição eletrônica de dados
Figura 2.11 Coletora de
dados Topcon FC-2500
®
utilizada para registrar,
armazenar e calcular
dados de estação total
eletrônica e GNSS.

Aquisição eletrônica de dados
• Limitações:
• Os dados podem ser apagados acidentalmente e
necessitam de baterias para o funcionamento;
• Geralmente não são a prova de água;
• Problemas de hardware e software.