
Cálculo de área de poligonais
Prof. Dr. Marcelo de Carvalho Alves
Departamento de Engenharia
Universidade Federal de Lavras
Lavras, MG

Introdução
• A determinação de áreas de poligonais é
importante para descrever a propriedade ou
detalhes de interesse dentro da propriedade,
bem como para fornecer suporte para cálculos de
volume.

• Vários métodos podem ser utilizados, tais como:
(1) divisão da gleba em figuras simples de
triângulos, retângulos e trapézios; (2) afastamento
a partir de uma linha reta; (3) cálculo de
coordenadas; (4) distâncias duplo-meridianas; (5)
contagem de pixels de uma imagem referente ao
mapa; (6) digitalização de coordenadas do mapa;
(7) e, aplicar um planímetro sobre o mapa.
Introdução

• Área do triângulo: A = (b . h)/2
• Área do retângulo: A = b . h
• Área do trapézio: A = (B + b)/2 . h
Cálculo de área por geometria
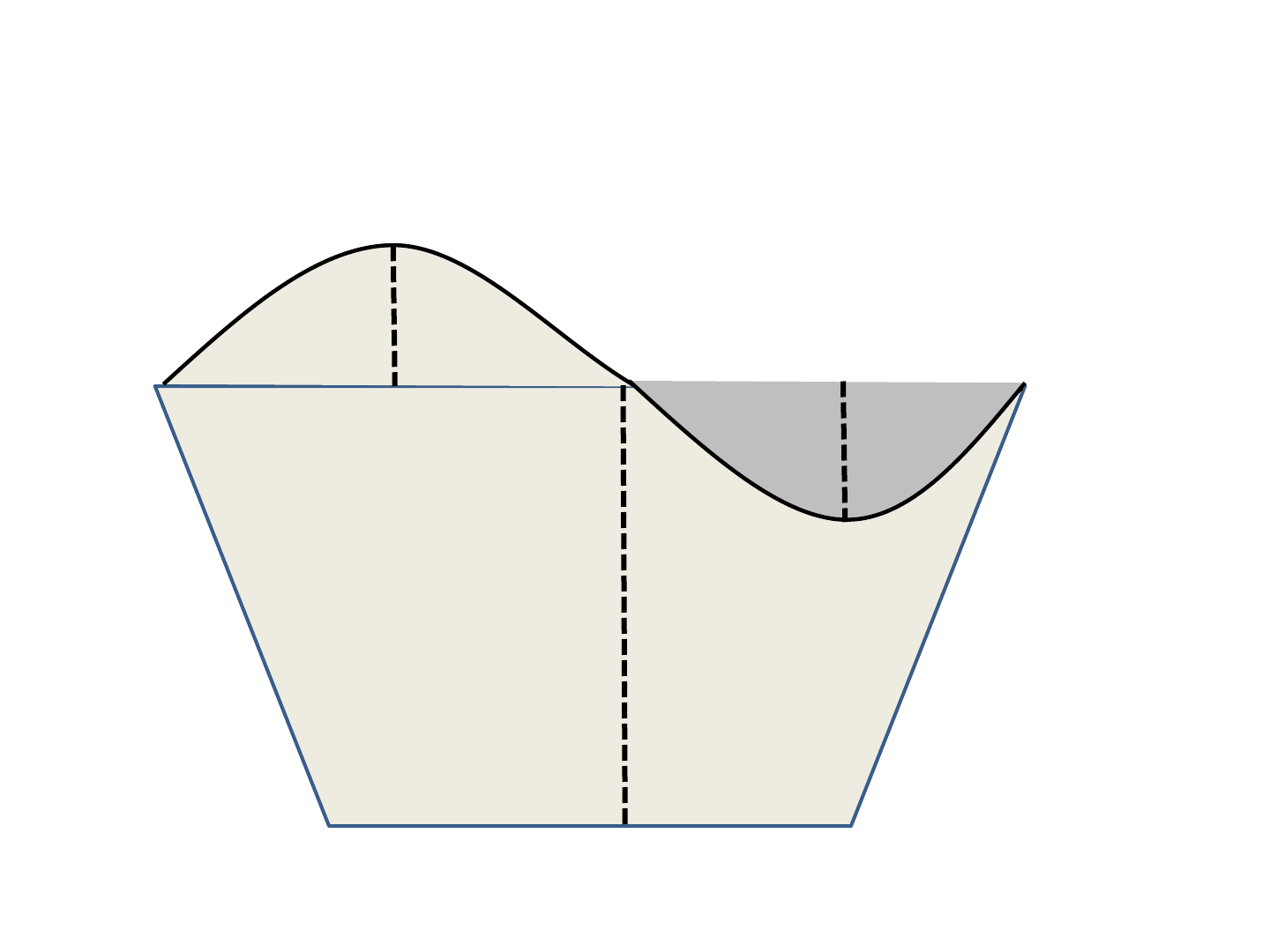
Cálculo de área por segmentos
parabólicos
f
h
A
B
C
D
E
F
G
Escala 1: 5000
A1
A2
A3

Cálculo de área por segmentos
parabólicos
• Área total = A1+A2-A3
• A1 = (8+6)/2 = 24,5cm
2
• Área dos segmentos parabólicos = A = 2/3.c.f
Em que, c é a corda e f, a flecha.

Cálculo de área por segmentos
parabólicos
• Se em A2, c = BD = 5 cm e f = 1,2 cm,
• A2 = (2/3) x 5 x 1,2 = 4 cm
2
• Se em A3, c = DF = 3 cm e f = 0,8 cm,
• A3 = 2/3 x 3 x 0,8 = 1,6 cm
2
• Atotal = 24,5 + 4 – 1,6 = 26,9 cm
2
, Considerando a
escala, AT = 26,9 x (5000)
2
= 67250 m
2
= 6,7250 ha

Cálculo de área por pesagem
• É necessário Balança de precisão + mapa impresso
• Ex: Um quadrado de 10 cm x 10 cm = 1,084g
O contorno topográfico = 21,792 g
Escala = 1: 500
100 cm
2
----1,084g
x ----21,792g x=2010,332 cm
2
Área = 2010,332 x (500)
2
= 50258,3m
2
= 5,2583ha

• O método de cálculo de área por coordenadas é o
mais utilizado.
• Esse método pode ser aplicado para cálculo
computacional de áreas de figuras em que as
coordenadas foram digitalizadas.
• Apenas uma equação pode ser aplicada para todas
as configurações geométricas de poligonais
fechadas.
Cálculo de área por coordenadas
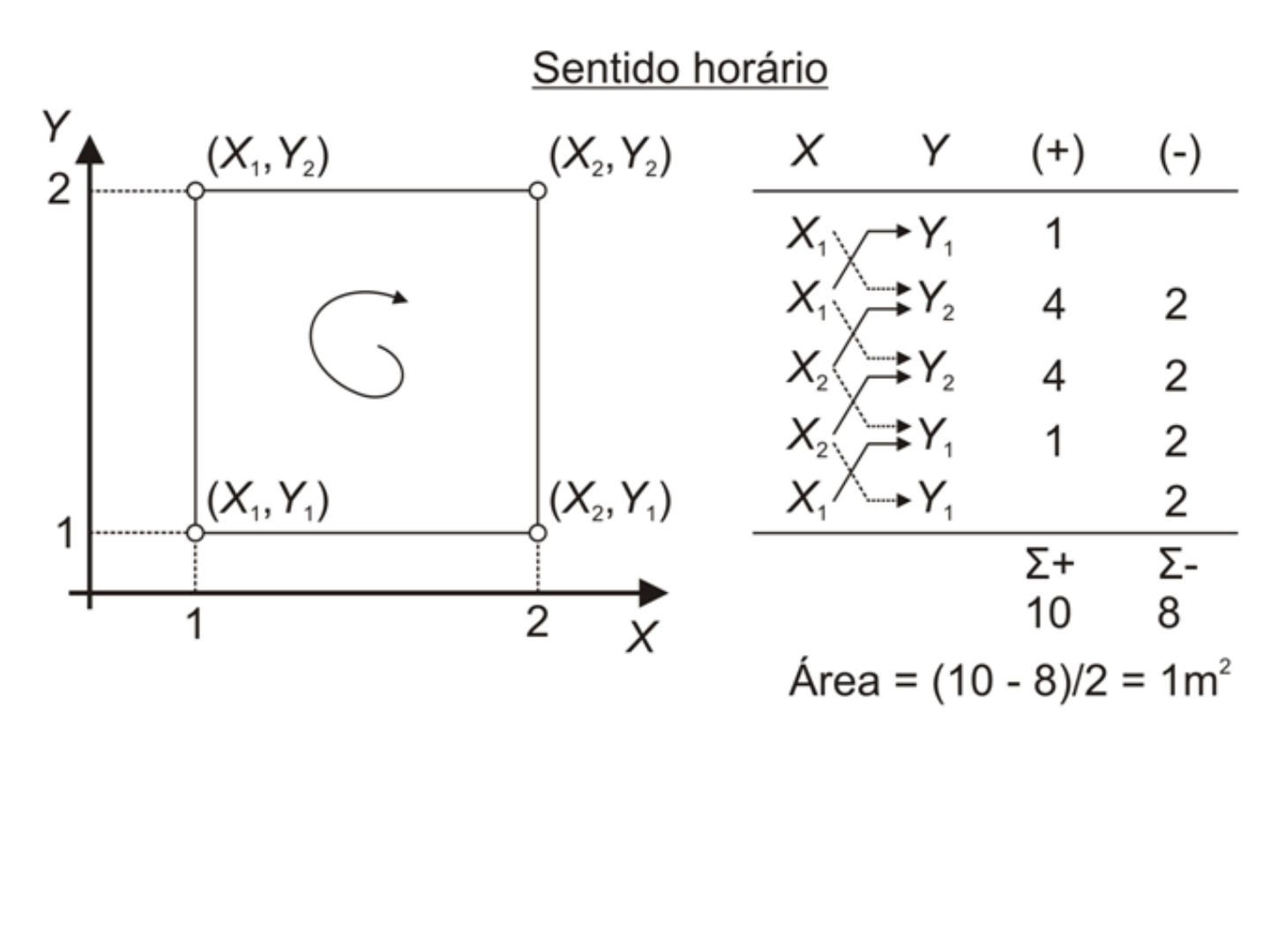
Cálculo de área pelo método de coordenadas cartesianas
dos vértices com caminhamento no sentido horário
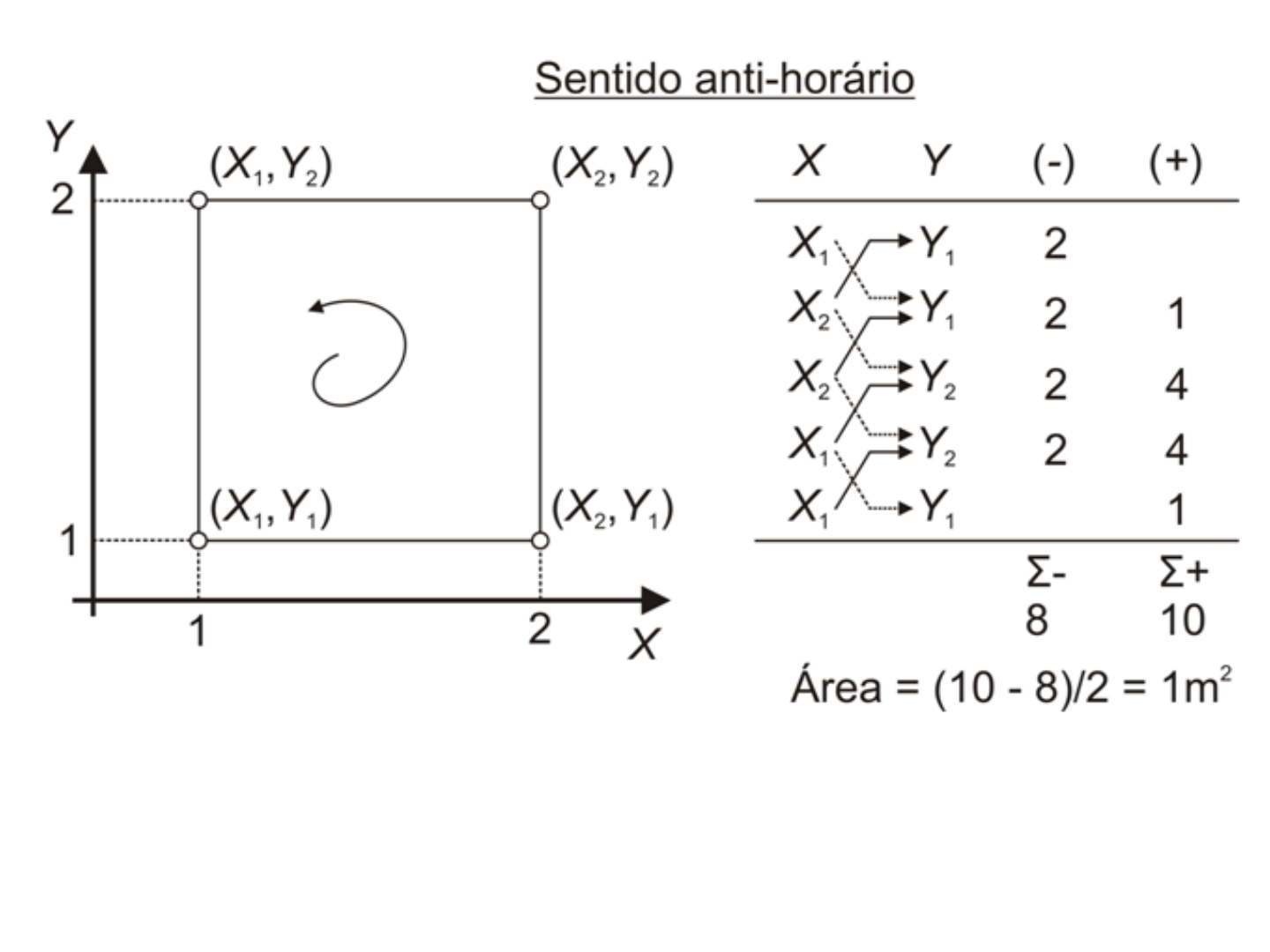
Cálculo de área pelo método de coordenadas cartesianas
dos vértices com caminhamento no sentido anti-horário

Cálculo analítico de área
• Utilizando a mesma figura anterior, com o
caminhamento no sentido horário, pode-se determinar
a área pelo processo analítico, de forma a se obter o
mesmo resultado.
• O processamento no sentido anti-horário, mudará
apenas a ordem da coluna dos resultados de área
dupla positiva ou negativa.
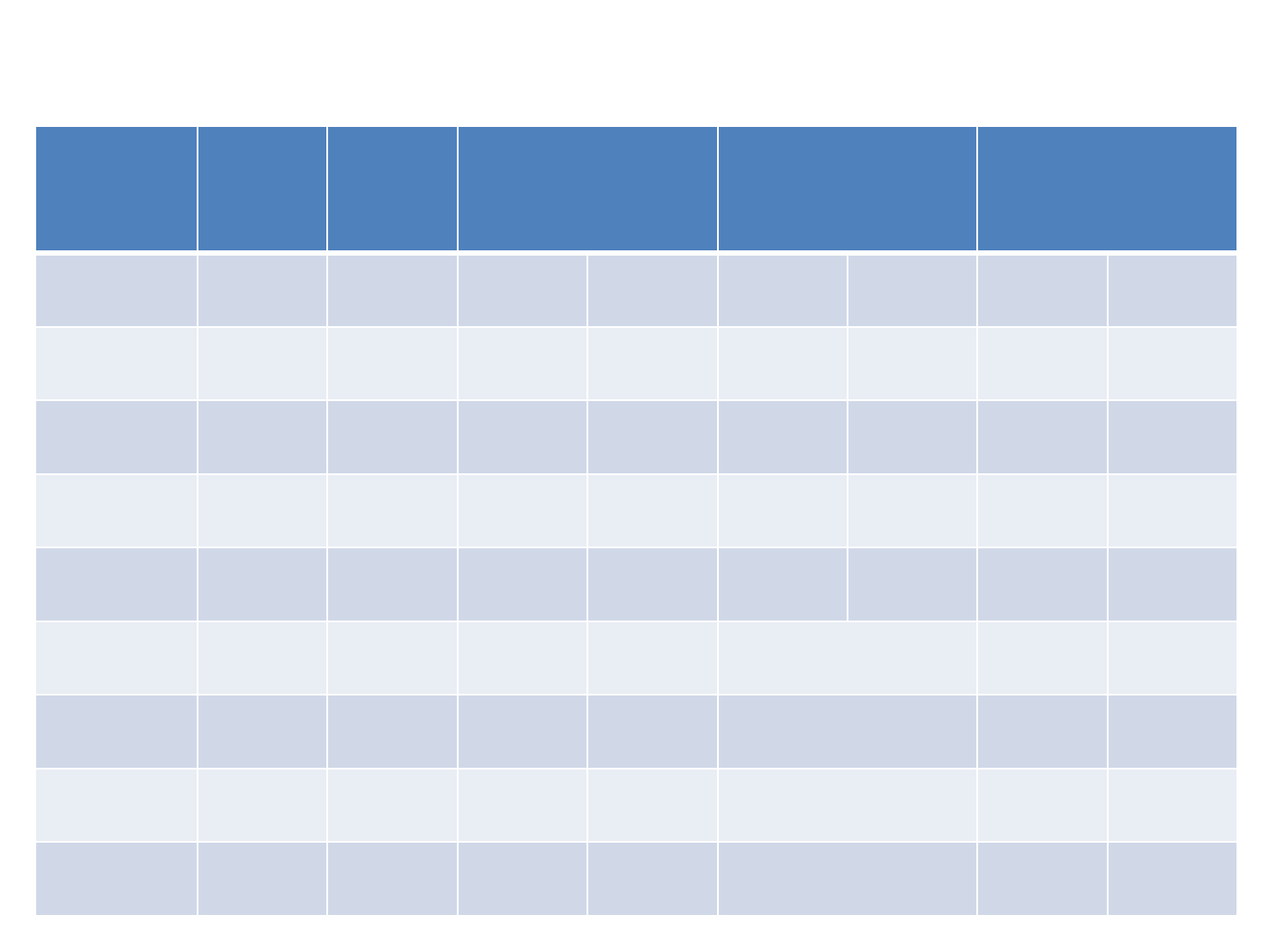
Cálculo analítico de área
Estação X Y Soma binária Diferença
binária
Área dupla
X Y X Y X.Y Y.X
A 1 1 2 3 0 -1 -2 0
B 1 2 3 4 -1 0 0 -4
C 2 2 4 3 0 1 4 0
D 2 1 3 2 1 0 0 2
Soma (+) +4 +2
Soma (-) -2 -4
Área dupla 2 -2
Área real 2/2= 1m
2

Áreas extrapoligonais
• Quando os pontos de uma poligonal são
escolhidos para o levantamento de uma
propriedade, procura-se acompanhar os limites
com a maior proximidade possível.
• No entanto, em algumas situações, não se pode
estabelecer a poligonal exatamente no limite, pois
há nas divisas cercas de arame, córregos, estradas
etc.
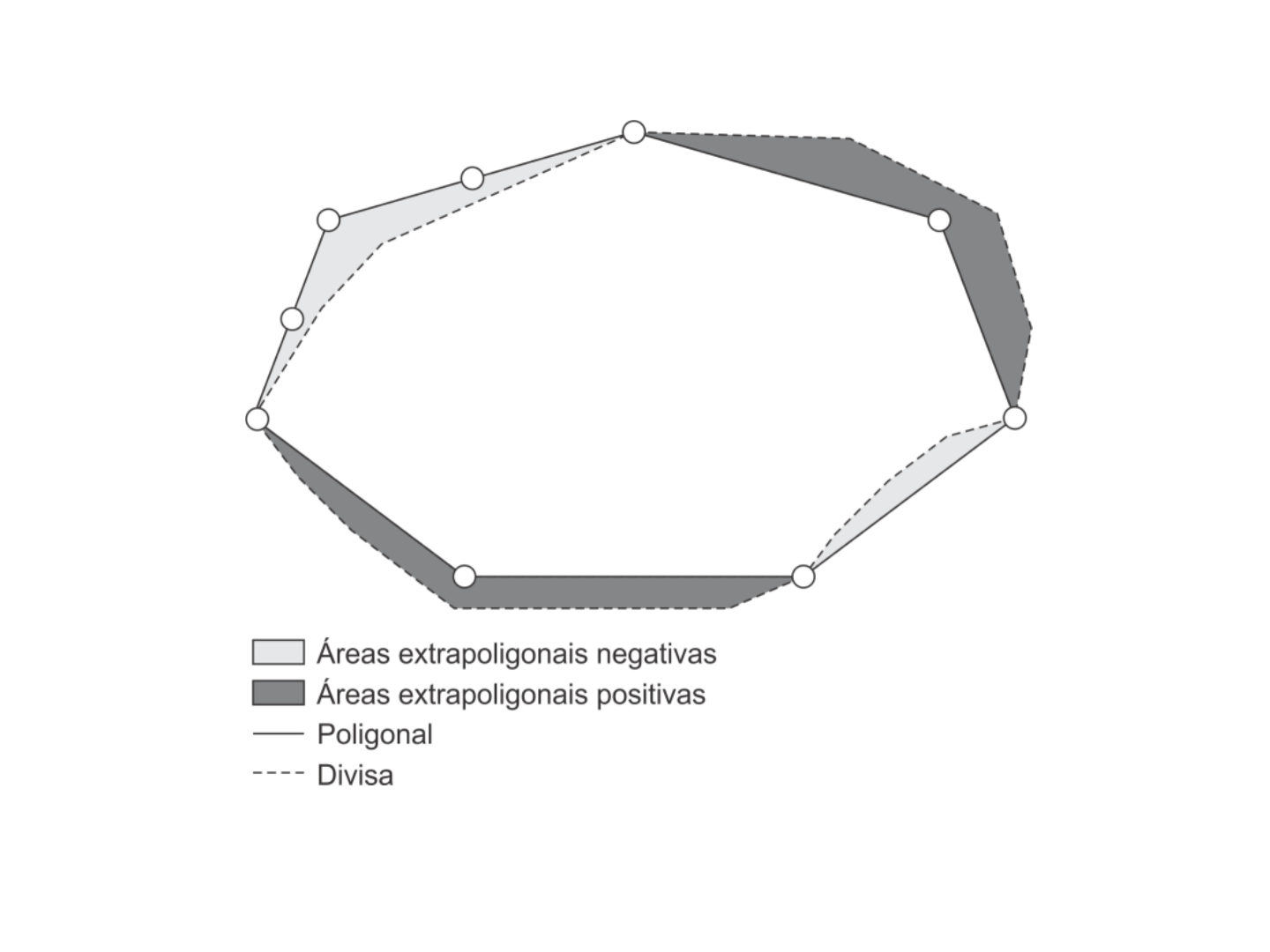
Áreas extrapoligonais
Poligonal com áreas extrapoligonais, em que a área final da propriedade será
a área da poligonal acrescida da somatória das áreas extrapoligonais
positivas e diminuída da somatória das áreas extrapoligonais negativas.

Método dos trapézios ou de Bezout
• Supõe-se uma sucessão de trapézios medidos ao
longo da poligonal, com o afastamento
perpendicular em distâncias fixas de 10 m em 10 m
ou de 20 m em 20 m.
• Os pontos A, B, C, D,..., n, são ligados por retas, de
forma que o cálculo não é rigorosamente exato.
• O uso de papel milimetrado pode facilitar o cálculo.
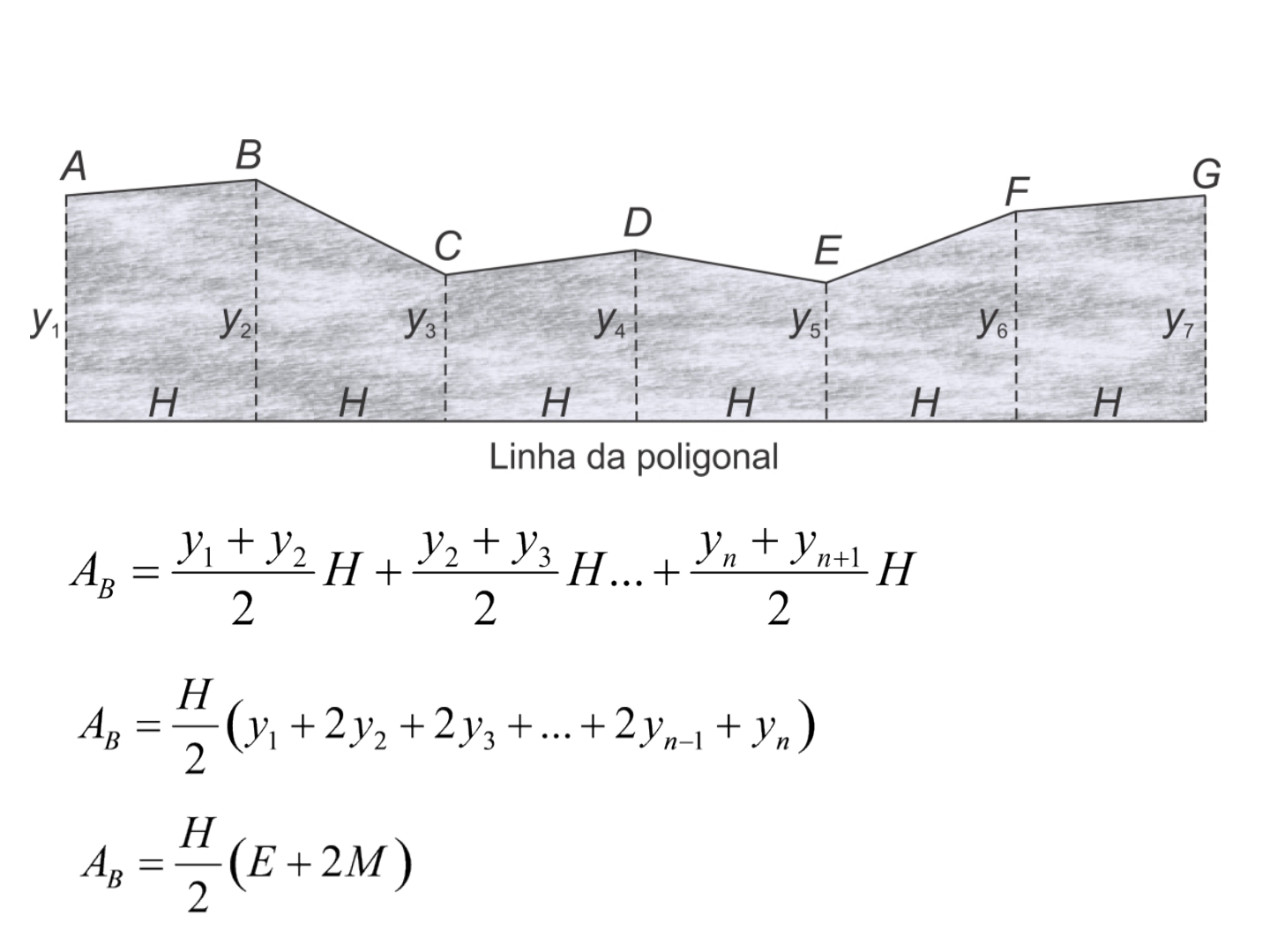
Método dos trapézios ou de Bezout
em que, os valores y extremos (E) são somados
uma vez e os y do meio ( M) são somados duas
vezes.

Método de Simpson
• Cada trecho de dois trapézios é considerado um
segmento de parábola, ou seja, ABC seria o
segmento de uma parábola, CDE o de outra, assim
por diante.
• Essa equação é um pouco mais complexa do que a
dos trapézios, porém parece mais correta quando
as divisas forem linhas curvas.
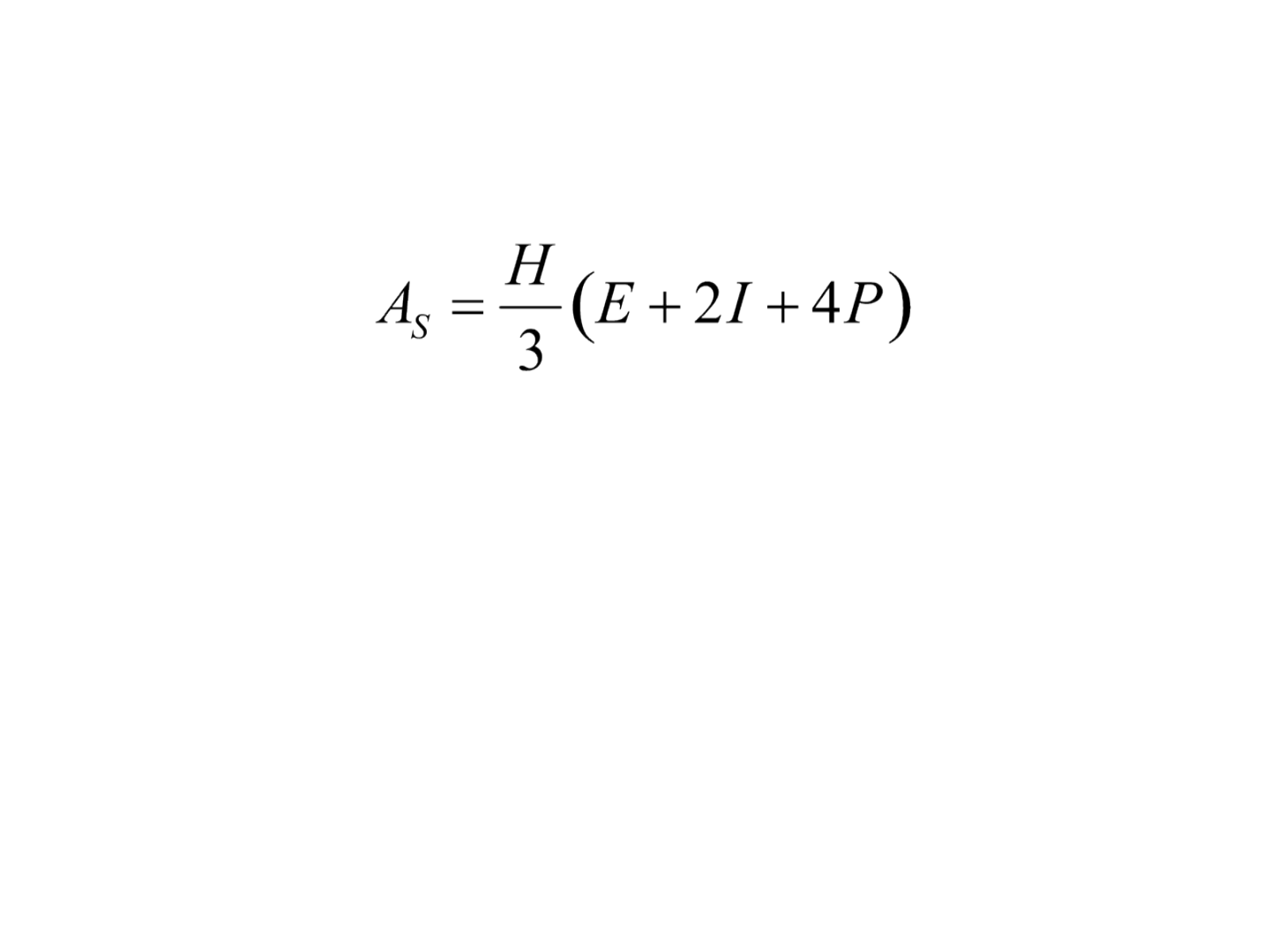
Método de Simpson
em que, E é a somatória dos y extremos, I , a somatória
dos y ímpares e, P dos y pares.
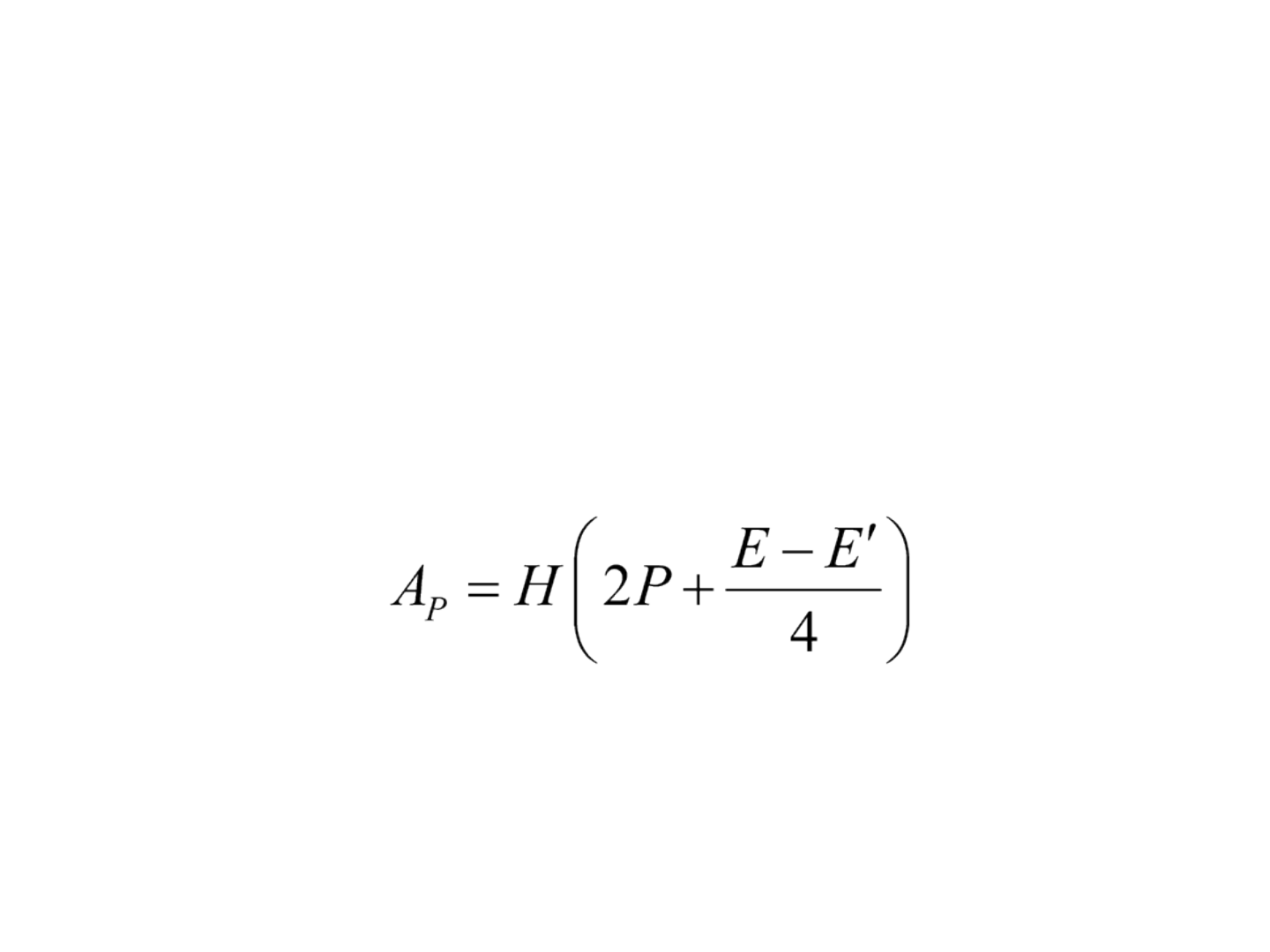
Método de Poncelet
• A idéia foi considerar duas áreas, sendo uma
formada com a poligonal e a outra com a tangete
aos pontos da poligonal.
• em que, E' é a somatória dos y adjacentes aos
extremos, ou seja, segundo e penúltimo y.

Aplicações da área no cálculo de
volume
• Conhecendo-se as áreas das seções transversais,
pode-se calcular o volume total de terra entre
cada seção, considerando que o volume de terra
entre as duas primeiras seções transversais é igual
ao volume de um prisma de bases A
1
e A
2
e altura
H.
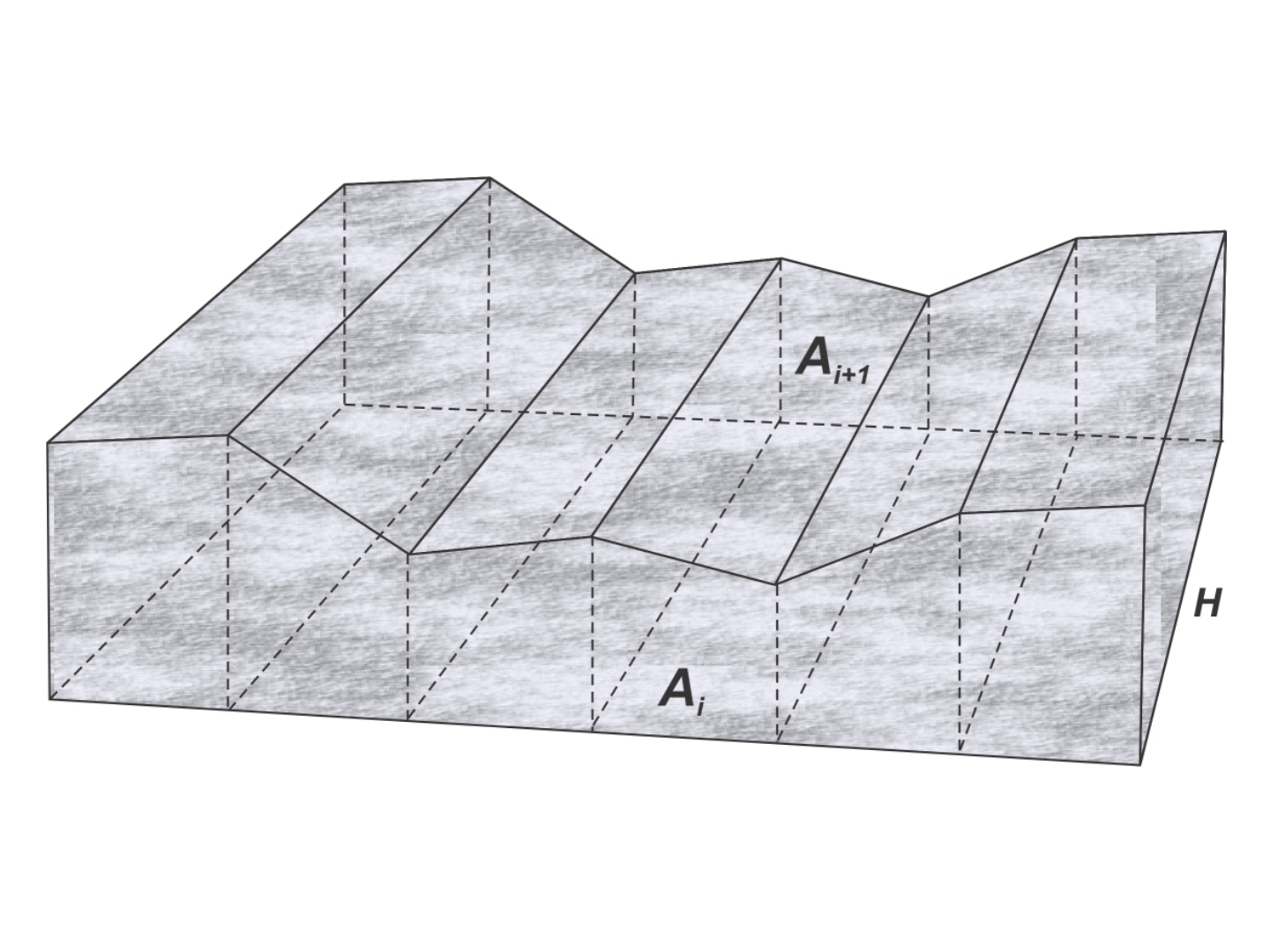
Cálculo de volume
Volume compreendido entre seções transversais
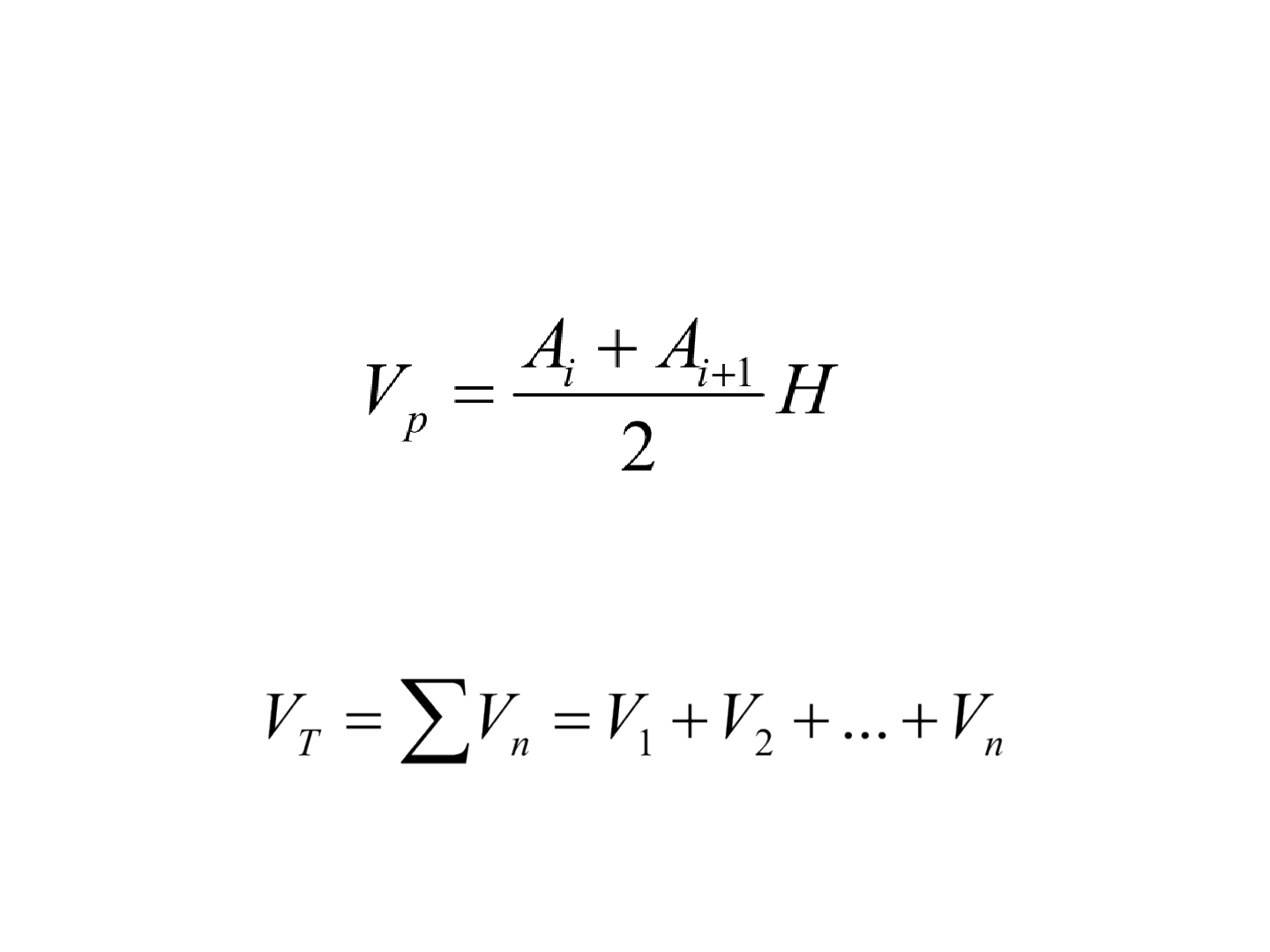
Cálculo de volume
• O volume parcial (V
p
) entre duas seções é:
• O volume total será a soma dos volumes parciais:

Cálculo de volume
• Em terraplenagem, uma das formas de pagamento
é o volume de terra movimentado.
• Assim, é necessário calcular o volume de corte a
ser efetuado.
• Deve-se, nesse caso, determinar a altura média do
terreno planificado em relação a um plano de
referência.
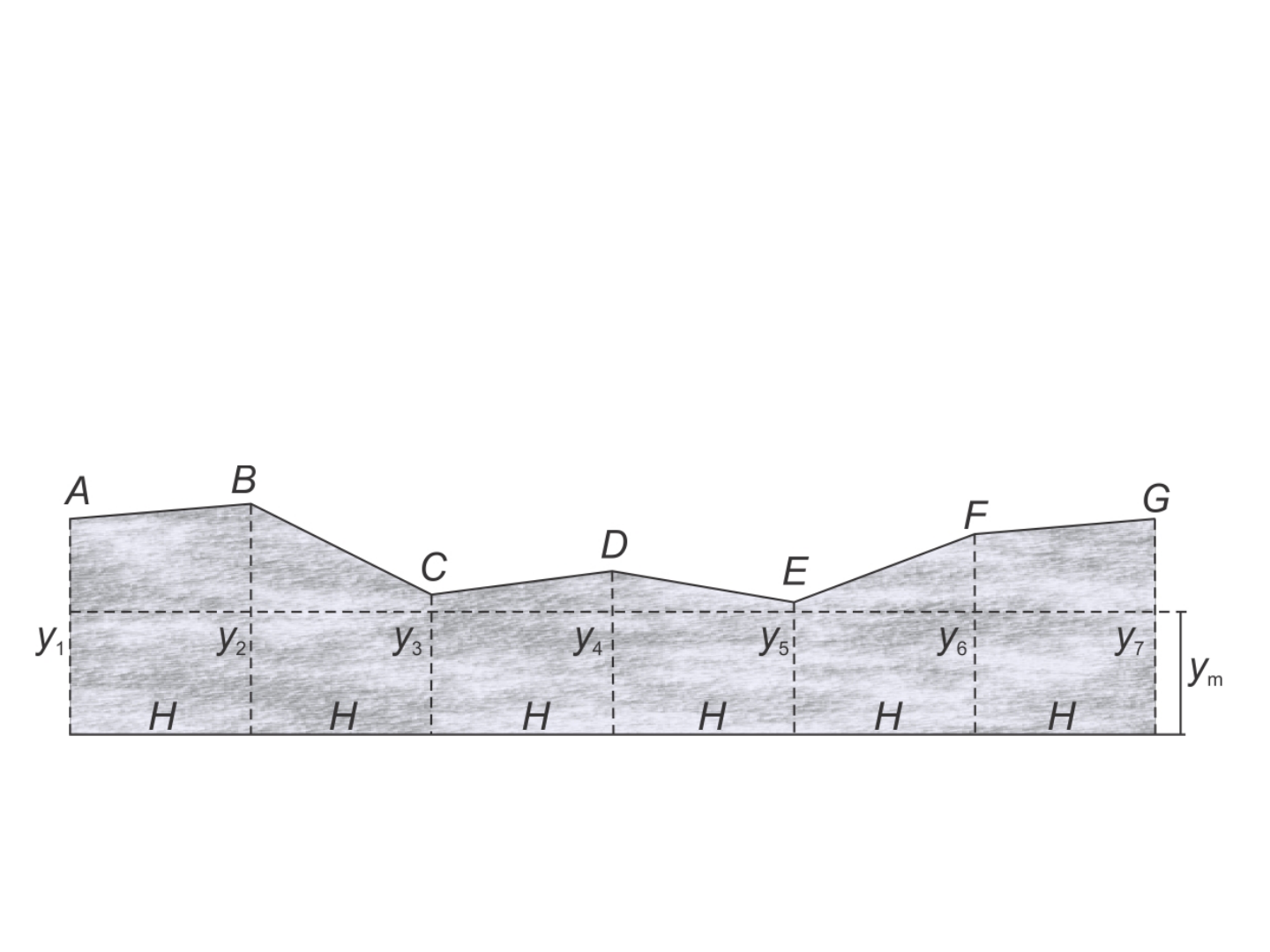
Cálculo de volume
• O plano de altura média determina em cada seção,
a área de corte (acima do plano) e de aterro
(abaixo do plano).
Definição da altura de corte do terreno para planificação.
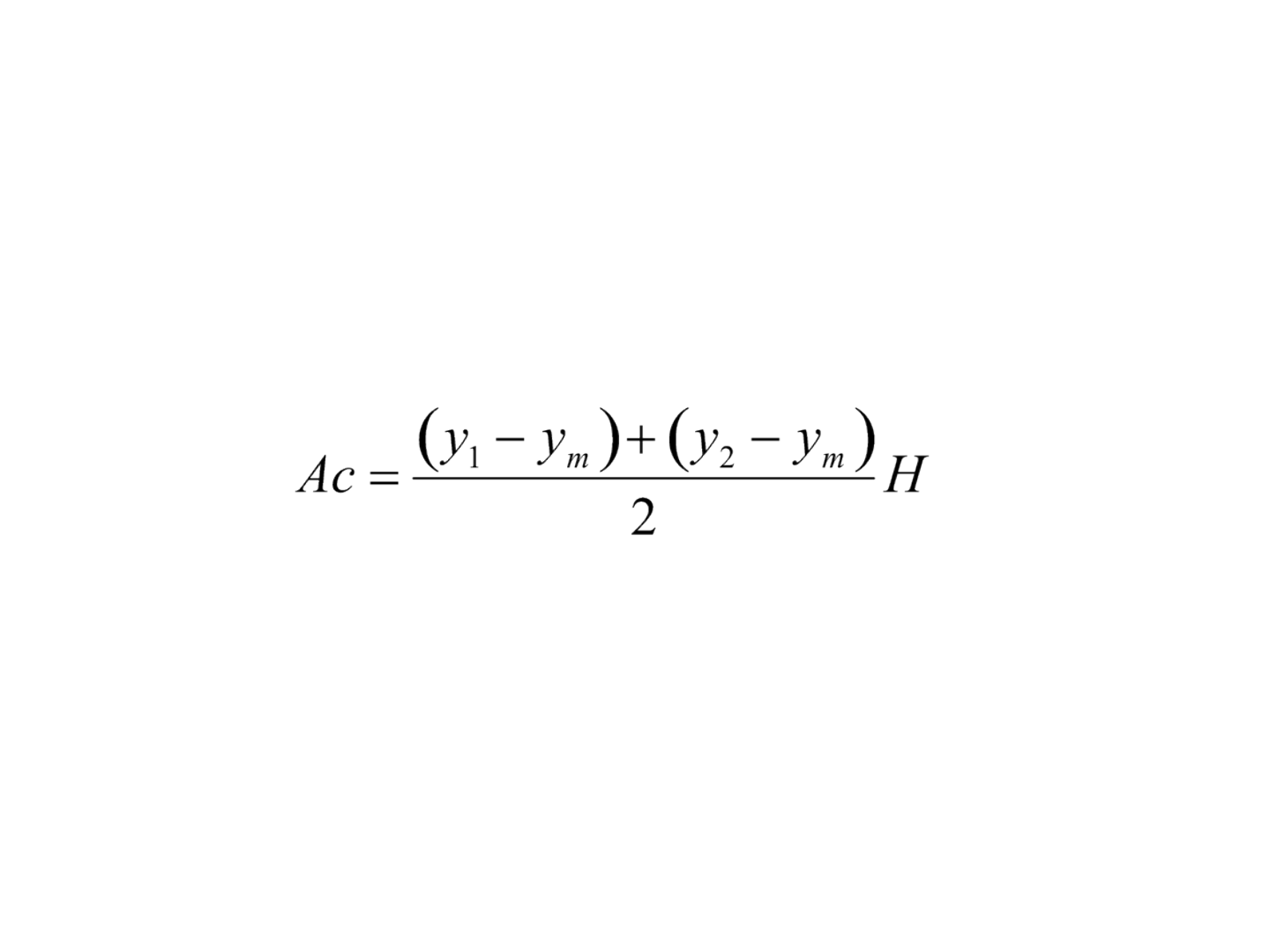
Cálculo de volume
• Considerando apenas uma seção, a área de corte
pode ser determinada por:
• em que, y
m
é a altura média do terreno planificado.
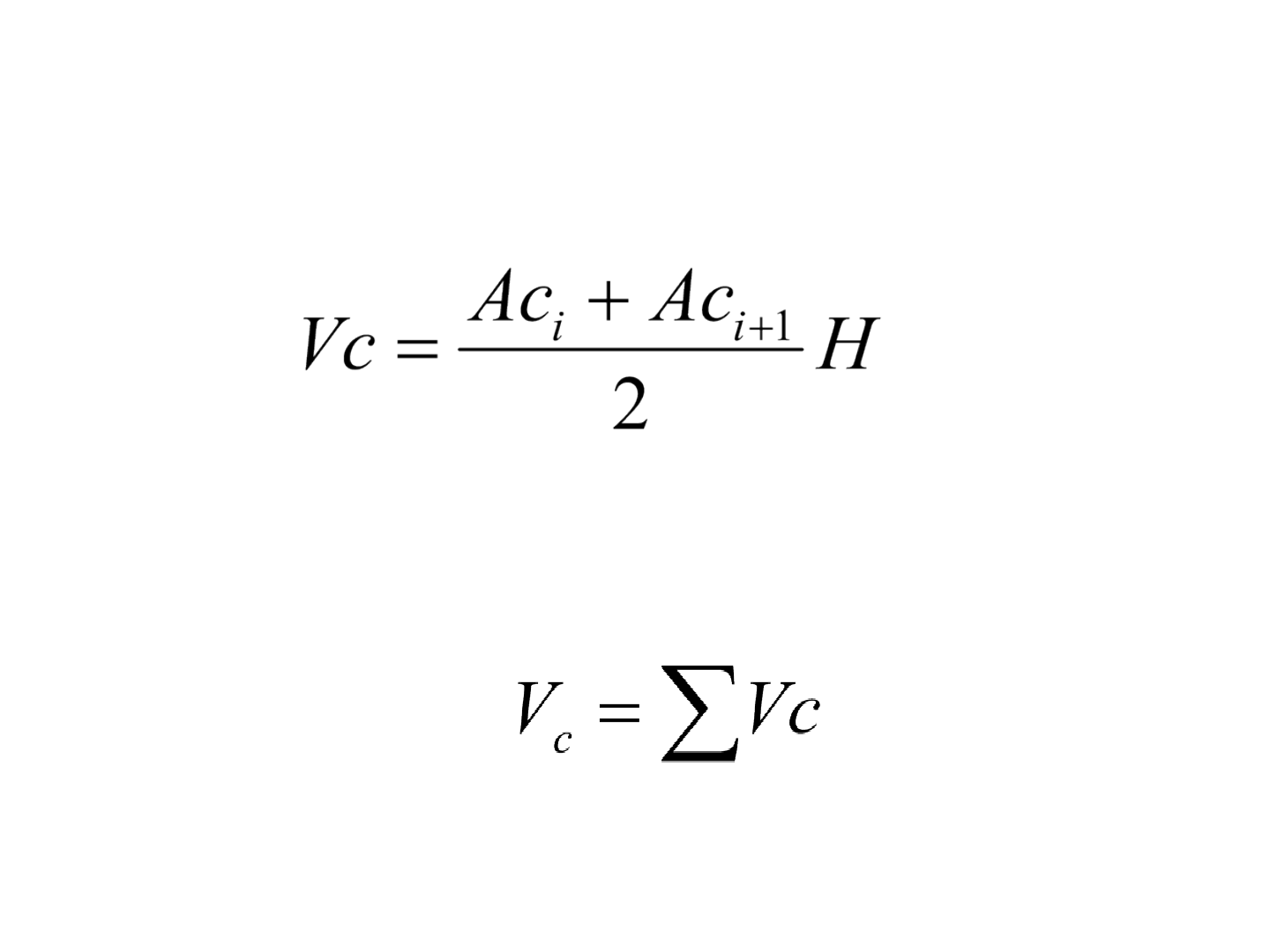
Cálculo de volume
• O volume de corte entre as seções seria:
• O volume de corte total seria

Fontes de erro em poligonação
• 1. Seleção inadequada de pontos de estação
resultando em condições inadequadas de visada
em função de (a) alternância de sol e sombra, (b)
visibilidade de apenas uma das extremidades da
linha, (c) linha de visada próxima ao solo, (d) linhas
que são muito curtas (e) e, visadas no sentido do
sol.
• 2. Erros em observar ângulos e distâncias.
• 3. Falha ao observar ângulos em números iguais de
vezes no sentido direto e inverso.

Enganos em poligonação e no
cálculo de poligonais
• 1. Ocupar o realizar visada em estação errada.
• 2. Orientação incorreta.
• 3. Confundir ângulos para a esquerda e direita.
• 4. Esquecer-se de registrar o ponto.
• 5. Não identificar a estação visada.

Enganos em poligonação e no
cálculo de poligonais
• 6. Falha em ajustar ângulos antes de calcular
azimutes ou rumos.
• 7. Aplicar ajustamento de ângulos na direção
errada e não chegar à soma de todos os ângulos.
• 8. Trocar valores de longitude e de latitude.
• 9. Confundir os sinais de coordenadas.